Mentioned In Dispatches

Wednesday, January 07, 2009

SICP Section 2.2 Hierarchical Data and the Closure Property - Part 1

Exercise 2.17. Define a procedure last-pair that returns the list that contains only the last element of a given (nonempty) list:

Answer: ~~This solution uses the length and list-ref functions described in the text.~~ Here is a simpler solution which does not use length or list-ref.

Exercise 2.18. Define a procedure reverse that takes a list as argument and returns a list of the same elements in reverse order:

Answer:

Exercise 2.19. Consider the change-counting program of section 1.2.2. It would be nice to be able to easily change the currency used by the program, so that we could compute the number of ways to change a British pound, for example. As the program is written, the knowledge of the currency is distributed partly into the procedure first-denomination and partly into the procedure count-change (which knows that there are five kinds of U.S. coins). It would be nicer to be able to supply a list of coins to be used for making change.

We want to rewrite the procedure cc so that its second argument is a list of the values of the coins to use rather than an integer specifying which coins to use. We could then have lists that defined each kind of currency:

We could then call cc as follows:

To do this will require changing the program cc somewhat. It will still have the same form, but it will access its second argument differently, as follows:

Define the procedures first-denomination, except-first-denomination, and no-more? in terms of primitive operations on list structures. Does the order of the list coin-values affect the answer produced by cc? Why or why not?

Answer:

Order of the list coin-values will not matter. This owes to the way cc is structured. The first recursive call to cc tries to compare the amount with *all* denominations irrespective of their order in the list.

Exercise 2.20. The procedures +, *, and list take arbitrary numbers of arguments. One way to define such procedures is to use define with dotted-tail notation. In a procedure definition, a parameter list that has a dot before the last parameter name indicates that, when the procedure is called, the initial parameters (if any) will have as values the initial arguments, as usual, but the final parameter's value will be a list of any remaining arguments. For instance, given the definition

the procedure f can be called with two or more arguments. If we evaluate

then in the body of f, x will be 1, y will be 2, and z will be the list (3 4 5 6). Given the definition

the procedure g can be called with zero or more arguments. If we evaluate

then in the body of g, w will be the list (1 2 3 4 5 6).

Use this notation to write a procedure same-parity that takes one or more integers and returns a list of all the arguments that have the same even-odd parity as the first argument. For example,

Answer:

Exercise 2.21. The procedure square-list takes a list of numbers as argument and returns a list of the squares of those numbers.

Here are two different definitions of square-list. Complete both of them by filling in the missing expressions:

Answer:

Exercise 2.22. Louis Reasoner tries to rewrite the first square-list procedure of exercise 2.21 so that it evolves an iterative process:

Unfortunately, defining square-list this way produces the answer list in the reverse order of the one desired. Why?

Louis then tries to fix his bug by interchanging the arguments to cons:

This doesn't work either. Explain.

Answer: In the first procedure iter starts by attaching the first item from the input list to answers. Subsequent items are consed to answers, thereby ending up *before* the first. Hence answers ends up having the square of the items in reverse order.

The second approach tried by Louis gets the order right. However the end result is not a plain list as he expects. Here the cons operation starts by attaching the empty answer list to the square of the first item. This yields (() . 1) and not (1). Further iterations repeat the same operation with similar results.

Exercise 2.23. The procedure for-each is similar to map. It takes as arguments a procedure and a list of elements. However, rather than forming a list of the results, for-each just applies the procedure to each of the elements in turn, from left to right. The values returned by applying the procedure to the elements are not used at all -- for-each is used with procedures that perform an action, such as printing. For example,

The value returned by the call to for-each (not illustrated above) can be something arbitrary, such as true. Give an implementation of for-each.

Answer:

Exercise 2.24. Suppose we evaluate the expression (list 1 (list 2 (list 3 4))). Give the result printed by the interpreter, the corresponding box-and-pointer structure, and the interpretation of this as a tree (as in figure 2.6). Answer: The interpreter prints (1 (2 (3 4))). I'll add the pictures once I draw them out using GIMP.

Exercise 2.25. Give combinations of cars and cdrs that will pick 7 from each of the following lists:

Answer:

Exercise 2.26. Suppose we define x and y to be two lists:

What result is printed by the interpreter in response to evaluating each of the following expressions:

Answer:

Exercise 2.27. Modify your reverse procedure of exercise 2.18 to produce a deep-reverse procedure that takes a list as argument and returns as its value the list with its elements reversed and with all sublists deep-reversed as well. For example,

Answer:

Exercise 2.28. Write a procedure fringe that takes as argument a tree (represented as a list) and returns a list whose elements are all the leaves of the tree arranged in left-to-right order. For example,

Answer:

Exercise 2.29. A binary mobile consists of two branches, a left branch and a right branch. Each branch is a rod of a certain length, from which hangs either a weight or another binary mobile. We can represent a binary mobile using compound data by constructing it from two branches (for example, using list):

A branch is constructed from a length (which must be a number) together with a structure, which may be either a number (representing a simple weight) or another mobile:

a. Write the corresponding selectors left-branch and right-branch, which return the branches of a mobile, and branch-length and branch-structure, which return the components of a branch.

b. Using your selectors, define a procedure total-weight that returns the total weight of a mobile.

c. A mobile is said to be balanced if the torque applied by its top-left branch is equal to that applied by its top-right branch (that is, if the length of the left rod multiplied by the weight hanging from that rod is equal to the corresponding product for the right side) and if each of the submobiles hanging off its branches is balanced. Design a predicate that tests whether a binary mobile is balanced.

d. Suppose we change the representation of mobiles so that the constructors are

How much do you need to change your programs to convert to the new representation?

Answer: a. As the mobile is represented as a list the selectors are straight forward to implement.

b. Calculation of total weight is made easier by an utility procedure which calculates the weight of a given branch. These procedure use mutual recursion to calculate the total weight of a given mobile.

c. The test to find out if a mobile is balanced can be similarly written with the help of an utility procedure to find out if its sub-mobiles are balanced.

d. Only the selectors need to be changed. For instance the right-branch can use (cdr mobile) instead of (car (cadr mobile)).

Exercise 2.30. Define a procedure square-tree analogous to the square-list procedure of exercise 2.21. That is, square-list should behave as follows:

Define square-tree both directly (i.e., without using any higher-order procedures) and also by using map and recursion.

Answer:

Exercise 2.31. Abstract your answer to exercise 2.30 to produce a procedure tree-map with the property that square-tree could be defined as

Answer:

Exercise 2.32. We can represent a set as a list of distinct elements, and we can represent the set of all subsets of the set as a list of lists. For example, if the set is (1 2 3), then the set of all subsets is (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3)). Complete the following definition of a procedure that generates the set of subsets of a set and give a clear explanation of why it works:

Answer:

Exercise 2.33. Fill in the missing expressions to complete the following definitions of some basic list-manipulation operations as accumulations:

Answer:

Exercise 2.34. Evaluating a polynomial in x at a given value of x can be formulated as an accumulation. We evaluate the polynomial

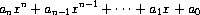
using a well-known algorithm called Horner's rule, which structures the computation as

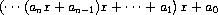
In other words, we start with an, multiply by x, add an-1, multiply by x, and so on, until we reach a0.16 Fill in the following template to produce a procedure that evaluates a polynomial using Horner's rule. Assume that the coefficients of the polynomial are arranged in a sequence, from a0 through an.

For example, to compute 1 + 3x + 5x³ + x⁵ at x = 2 you would evaluate

Answer:

Exercise 2.35. Redefine count-leaves from section 2.2.2 as an accumulation:

Answer:

Exercise 2.36. The procedure accumulate-n is similar to accumulate except that it takes as its third argument a sequence of sequences, which are all assumed to have the same number of elements. It applies the designated accumulation procedure to combine all the first elements of the sequences, all the second elements of the sequences, and so on, and returns a sequence of the results. For instance, if s is a sequence containing four sequences, ((1 2 3) (4 5 6) (7 8 9) (10 11 12)), then the value of (accumulate-n + 0 s) should be the sequence (22 26 30). Fill in the missing expressions in the following definition of accumulate-n:

Answer:

Exercise 2.37. Suppose we represent vectors v = (vi) as sequences of numbers, and matrices m = (mij) as sequences of vectors (the rows of the matrix). For example, the matrix

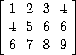
is represented as the sequence ((1 2 3 4) (4 5 6 6) (6 7 8 9)). With this representation, we can use sequence operations to concisely express the basic matrix and vector operations. These operations (which are described in any book on matrix algebra) are the following:

We can define the dot product as

Fill in the missing expressions in the following procedures for computing the other matrix operations. (The procedure accumulate-n is defined in exercise 2.36.)

Answer:

Exercise 2.38. The accumulate procedure is also known as fold-right, because it combines the first element of the sequence with the result of combining all the elements to the right. There is also a fold-left, which is similar to fold-right, except that it combines elements working in the opposite direction:

What are the values of

Give a property that op should satisfy to guarantee that fold-right and fold-left will produce the same values for any sequence.

Answer:

In order for fold-right and fold-left to yield identical results op should be associative. For instance take the + operator.

Exercise 2.39. Complete the following definitions of reverse (exercise 2.18) in terms of fold-right and fold-left from exercise 2.38:

Answer:

Exercise 2.40. Define a procedure unique-pairs that, given an integer n, generates the sequence of pairs (i,j) with 1< j< i< n. Use unique-pairs to simplify the definition of prime-sum-pairs given above.

Answer:

Exercise 2.41. Write a procedure to find all ordered triples of distinct positive integers i, j, and k less than or equal to a given integer n that sum to a given integer s.

Answer:

Exercise 2.42.

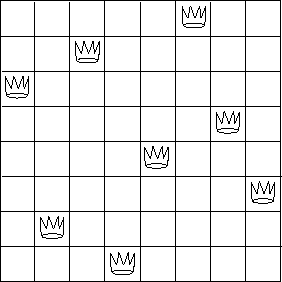
Figure 2.8: A solution to the eight-queens puzzle.

The ``eight-queens puzzle'' asks how to place eight queens on a chessboard so that no queen is in check from any other (i.e., no two queens are in the same row, column, or diagonal). One possible solution is shown in figure 2.8. One way to solve the puzzle is to work across the board, placing a queen in each column. Once we have placed k - 1 queens, we must place the kth queen in a position where it does not check any of the queens already on the board. We can formulate this approach recursively: Assume that we have already generated the sequence of all possible ways to place k - 1 queens in the first k - 1 columns of the board. For each of these ways, generate an extended set of positions by placing a queen in each row of the kth column. Now filter these, keeping only the positions for which the queen in the kth column is safe with respect to the other queens. This produces the sequence of all ways to place k queens in the first k columns. By continuing this process, we will produce not only one solution, but all solutions to the puzzle.

We implement this solution as a procedure queens, which returns a sequence of all solutions to the problem of placing n queens on an n× n chessboard. Queens has an internal procedure queen-cols that returns the sequence of all ways to place queens in the first k columns of the board.

In this procedure rest-of-queens is a way to place k - 1 queens in the first k - 1 columns, and new-row is a proposed row in which to place the queen for the kth column. Complete the program by implementing the representation for sets of board positions, including the procedure adjoin-position, which adjoins a new row-column position to a set of positions, and empty-board, which represents an empty set of positions. You must also write the procedure safe?, which determines for a set of positions, whether the queen in the kth column is safe with respect to the others. (Note that we need only check whether the new queen is safe -- the other queens are already guaranteed safe with respect to each other.)

Answer:

(define empty-board (list nil))

(define (adjoin-position new-row k rest-of-queens)
  (if (null? (car rest-of-queens))
      (list (list k new-row))
      (cons (list k new-row) rest-of-queens)))

(define (safe? k positions)
  (define (iter new-pos others)
    (if (null? others) #t
        (let ((other-pos (car others)))
          (if (row-col-or-dia-matches? new-pos other-pos) #f
              (iter new-pos (cdr others))))))
  (if (= k 1) #t
      (iter (car positions) (cdr positions))))
             
(define (row-col-or-dia-matches? new-position other-position)
  (or (same-row? new-position other-position)
      (same-col? new-position other-position)
      (same-diagonal? new-position other-position)))
          
(define (same-row? pos1 pos2)
  (= (cadr pos1) (cadr pos2)))
  
(define (same-col? pos1 pos2)
  (= (car pos1) (car pos2)))

(define (same-diagonal? pos1 pos2)
  (let ((k1 (car pos1))
        (k2 (car pos2))
        (r1 (cadr pos1))        
        (r2 (cadr pos2)))
    (= (abs (- k1 k2))
       (abs (- r1 r2)))))

Exercise 2.43. Louis Reasoner is having a terrible time doing exercise 2.42. His queens procedure seems to work, but it runs extremely slowly. (Louis never does manage to wait long enough for it to solve even the 6× 6 case.) When Louis asks Eva Lu Ator for help, she points out that he has interchanged the order of the nested mappings in the flatmap, writing it as

Explain why this interchange makes the program run slowly. Estimate how long it will take Louis's program to solve the eight-queens puzzle, assuming that the program in exercise 2.42 solves the puzzle in time T.

Answer: Louis is breaking a well known rule of thumb in programming - namely to avoid expensive operations in inner loops. His code is calling the expensive recursive call to queen-cols in the inner loop.

I am not able to figure out how much time Louis' procedure will take to run in terms of T. If you have an answer/explanation do let me know.

Saturday, December 27, 2008

SICP Section 2.1 Introduction to Data Abstraction

Exercise 2.1. Define a better version of make-rat that handles both positive and negative arguments. Make-rat should normalize the sign so that if the rational number is positive, both the numerator and denominator are positive, and if the rational number is negative, only the numerator is negative.

Answer:

Exercise 2.2. Consider the problem of representing line segments in a plane. Each segment is represented as a pair of points: a starting point and an ending point. Define a constructor make-segment and selectors start-segment and end-segment that define the representation of segments in terms of points. Furthermore, a point can be represented as a pair of numbers: the x coordinate and the y coordinate. Accordingly, specify a constructor make-point and selectors x-point and y-point that define this representation. Finally, using your selectors and constructors, define a procedure midpoint-segment that takes a line segment as argument and returns its midpoint (the point whose coordinates are the average of the coordinates of the endpoints). To try your procedures, you'll need a way to print points:

Answer:

Exercise 2.3. Implement a representation for rectangles in a plane. (Hint: You may want to make use of exercise 2.2.) In terms of your constructors and selectors, create procedures that compute the perimeter and the area of a given rectangle. Now implement a different representation for rectangles. Can you design your system with suitable abstraction barriers, so that the same perimeter and area procedures will work using either representation?

Answer:

Exercise 2.4. Here is an alternative procedural representation of pairs. For this representation, verify that (car (cons x y)) yields x for any objects x and y.

What is the corresponding definition of cdr? (Hint: To verify that this works, make use of the substitution model of section 1.1.5.)

Answer:

Exercise 2.5. Show that we can represent pairs of nonnegative integers using only numbers and arithmetic operations if we represent the pair a and b as the integer that is the product 2a 3b. Give the corresponding definitions of the procedures cons, car, and cdr.

Answer:

Exercise 2.6. In case representing pairs as procedures wasn't mind-boggling enough, consider that, in a language that can manipulate procedures, we can get by without numbers (at least insofar as nonnegative integers are concerned) by implementing 0 and the operation of adding 1 as

This representation is known as Church numerals, after its inventor, Alonzo Church, the logician who invented the calculus.

Define one and two directly (not in terms of zero and add-1). (Hint: Use substitution to evaluate (add-1 zero)). Give a direct definition of the addition procedure + (not in terms of repeated application of add-1).

Answer:

Exercise 2.7. Alyssa's program is incomplete because she has not specified the implementation of the interval abstraction. Here is a definition of the interval constructor:

Define selectors upper-bound and lower-bound to complete the implementation.

Answer:

Exercise 2.8. Using reasoning analogous to Alyssa's, describe how the difference of two intervals may be computed. Define a corresponding subtraction procedure, called sub-interval.

Answer:

Exercise 2.10. Ben Bitdiddle, an expert systems programmer, looks over Alyssa's shoulder and comments that it is not clear what it means to divide by an interval that spans zero. Modify Alyssa's code to check for this condition and to signal an error if it occurs.

Exercise 2.11. In passing, Ben also cryptically comments: ``By testing the signs of the endpoints of the intervals, it is possible to break mul-interval into nine cases, only one of which requires more than two multiplications.'' Rewrite this procedure using Ben's suggestion.

After debugging her program, Alyssa shows it to a potential user, who complains that her program solves the wrong problem. He wants a program that can deal with numbers represented as a center value and an additive tolerance; for example, he wants to work with intervals such as 3.5± 0.15 rather than [3.35, 3.65]. Alyssa returns to her desk and fixes this problem by supplying an alternate constructor and alternate selectors:

Unfortunately, most of Alyssa's users are engineers. Real engineering situations usually involve measurements with only a small uncertainty, measured as the ratio of the width of the interval to the midpoint of the interval. Engineers usually specify percentage tolerances on the parameters of devices, as in the resistor specifications given earlier.

Answer:

(define (above-zero? interval)
  (and (> (lower-bound interval) 0)
       (> (upper-bound interval) 0)))

(define (below-zero? interval)
  (and (< (lower-bound interval) 0)
       (< (upper-bound interval) 0)))

(define (mul-interval x y)
  (let ((l1l2 (* (lower-bound x) (lower-bound y)))
        (l1u2 (* (lower-bound x) (upper-bound y)))
        (u1l2 (* (upper-bound x) (lower-bound y)))
        (u1u2 (* (upper-bound x) (upper-bound y))))
    (cond ((and (above-zero? x) (above-zero? y))
            (make-interval l1l2 u1u2))
           
           ((and (above-zero? x) (spans-zero? y))
            (make-interval u1l2 u1u2))
           
           ((and (spans-zero? x) (above-zero? y))
            (make-interval l1u2 u1u2))
           
           ((and (above-zero? x) (below-zero? y))
            (make-interval u1u2 l1l2))
           
           ((and (below-zero? x) (above-zero? y))
            (make-interval u1u2 l1l2))
           
           ((and (below-zero? x) (spans-zero? y))
            (make-interval l1u2 l1l2))
           
           ((and (spans-zero? x) (below-zero? y))
            (make-interval u1l2 l1l2))
           
           ((and (below-zero? x) (below-zero? y))
            (make-interval u1u2 l1l2))
           
           ((and (spans-zero? x) (spans-zero? y))
            (make-interval (min l1u2 u1l2) (min l1l2 u1u2))))))

Exercise 2.12. Define a constructor make-center-percent that takes a center and a percentage tolerance and produces the desired interval. You must also define a selector percent that produces the percentage tolerance for a given interval. The center selector is the same as the one shown above.

Answer:

Exercise 2.13. Show that under the assumption of small percentage tolerances there is a simple formula for the approximate percentage tolerance of the product of two intervals in terms of the tolerances of the factors. You may simplify the problem by assuming that all numbers are positive.

After considerable work, Alyssa P. Hacker delivers her finished system. Several years later, after she has forgotten all about it, she gets a frenzied call from an irate user, Lem E. Tweakit. It seems that Lem has noticed that the formula for parallel resistors can be written in two algebraically equivalent ways:

and

He has written the following two programs, each of which computes the parallel-resistors formula differently:

Lem complains that Alyssa's program gives different answers for the two ways of computing. This is a serious complaint.

Answer: Let x and y be two intervals and dx and dy their respective tolerances. Their product can be calculated as (x + dx) * (y + dy). Expanding this we get xy + xdy + ydx + dxdy. As dx and dy are small to begin with their product will be very small and can be ignored without losing much accuracy. The equation then becomes xy + xdy + ydx.

If we call the product z, with a tolerance dz, then z + dz = xy + xdy + ydx. Separating z and dz, we get dz = xdy + ydx. This is the relation between the tolerance of the product the individual tolerances.

Exercise 2.14. Demonstrate that Lem is right. Investigate the behavior of the system on a variety of arithmetic expressions. Make some intervals A and B, and use them in computing the expressions A/A and A/B. You will get the most insight by using intervals whose width is a small percentage of the center value. Examine the results of the computation in center-percent form (see exercise 2.12).

Answer: Lem's hypothesis is easily proven right. Take the example below.

The problem stems from the fact that the formulae do not take intervals into consideration whereas the code does. For instance the interval one implicitly assumes that R1/R1 = R2/R2 = 1. However this is only true when intervals are not involved. Hence the two formulae give two different results.

Exercise 2.15. Eva Lu Ator, another user, has also noticed the different intervals computed by different but algebraically equivalent expressions. She says that a formula to compute with intervals using Alyssa's system will produce tighter error bounds if it can be written in such a form that no variable that represents an uncertain number is repeated. Thus, she says, par2 is a ``better'' program for parallel resistances than par1. Is she right? Why?

Answer: Eva is correct. As we are operating with intervals rather than whole numbers it is better to reduce the "occurrence" of intervals in any given formula to a minimum. This reduces the number of ways in which errors can creep in and thereby produces tighter bounds. As the second formula has fewer occurrences of the intervals it will produce tighter bounds.

Exercise 2.16. Explain, in general, why equivalent algebraic expressions may lead to different answers. Can you devise an interval-arithmetic package that does not have this shortcoming, or is this task impossible? (Warning: This problem is very difficult.)

Answer: The answer is similar those of the two previous questions. The main reason is the difference between using whole numbers and intervals. Normal properties and rules of algebra that apply to whole numbers do not hold true when intervals are used. For instance, while x/x = 1 when x and y are non zero whole numbers this is not so for cases when x is an interval. Likewise x - x need not be zero and so on.

It *might* be possible to develop a package provided such concepts as inverse can be defined for an interval. I am not sure how to go about the definitions though.

Tuesday, December 23, 2008

SICP Section 1.3 Formulating Abstractions with Higher-Order Procedures

Exercise 1.29. Simpson's Rule is a more accurate method of numerical integration than the method illustrated above. Using Simpson's Rule, the integral of a function f between a and b is approximated as

where h = (b - a)/n, for some even integer n, and yk = f(a + kh). (Increasing n increases the accuracy of the approximation.) Define a procedure that takes as arguments f, a, b, and n and returns the value of the integral, computed using Simpson's Rule. Use your procedure to integrate cube between 0 and 1 (with n = 100 and n = 1000), and compare the results to those of the integral procedure shown above.

Answer:

Exercise 1.30. The sum procedure above generates a linear recursion. The procedure can be rewritten so that the sum is performed iteratively. Show how to do this by filling in the missing expressions in the following definition:

Answer:

Exercise 1.31. a. The sum procedure is only the simplest of a vast number of similar abstractions that can be captured as higher-order procedures. Write an analogous procedure called product that returns the product of the values of a function at points over a given range. Show how to define factorial in terms of product. Also use product to compute approximations to using the formula

b. If your product procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.

Answer:

Exercise 1.32. a. Show that sum and product (exercise 1.31) are both special cases of a still more general notion called accumulate that combines a collection of terms, using some general accumulation function:

Accumulate takes as arguments the same term and range specifications as sum and product, together with a combiner procedure (of two arguments) that specifies how the current term is to be combined with the accumulation of the preceding terms and a null-value that specifies what base value to use when the terms run out. Write accumulate and show how sum and product can both be defined as simple calls to accumulate.
b. If your accumulate procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.

Answer

Exercise 1.33. You can obtain an even more general version of accumulate (exercise 1.32) by introducing the notion of a filter on the terms to be combined. That is, combine only those terms derived from values in the range that satisfy a specified condition. The resulting filtered-accumulate abstraction takes the same arguments as accumulate, together with an additional predicate of one argument that specifies the filter. Write filtered-accumulate as a procedure. Show how to express the following using filtered-accumulate:

a. the sum of the squares of the prime numbers in the interval a to b (assuming that you have a prime? predicate already written)

b. the product of all the positive integers less than n that are relatively prime to n (i.e., all positive integers i < n such that GCD(i,n) = 1).

Answer:

Exercise 1.34. Suppose we define the procedure

Then we have

What happens if we (perversely) ask the interpreter to evaluate the combination (f f)? Explain.

Answer: f is a procedure that accepts another procedure g as its argument. When executed f calls g, passing 2 as argument. In the first example the argument procedure is square. When square is called with 2 as its argument the result is naturally 4.

When we try to call f passing itself as an argument the following things happen:

The first time f receives a procedure, f, as its argument.
The argument is then invoked, passing 2 as a parameter. As the argument is f itself, this means invoking (f 2)
The argument to f now is 2, leading to (2 2) being invoked. This causes as the interpreter expects the first item in the expression to be a procedure but instead gets 2.

Exercise 1.35. Show that the golden ratio (section 1.2.2) is a fixed point of the transformation x 1 + 1/x, and use this fact to compute by means of the fixed-point procedure.

Answer:

Exercise 1.36. Modify fixed-point so that it prints the sequence of approximations it generates, using the newline and display primitives shown in exercise 1.22. Then find a solution to xx = 1000 by finding a fixed point of x log(1000)/log(x). (Use Scheme's primitive log procedure, which computes natural logarithms.) Compare the number of steps this takes with and without average damping. (Note that you cannot start fixed-point with a guess of 1, as this would cause division by log(1) = 0.)

Answer:

Exercise 1.37. a. An infinite continued fraction is an expression of the form

As an example, one can show that the infinite continued fraction expansion with the Ni and the Di all equal to 1 produces 1/, where is the golden ratio (described in section 1.2.2). One way to approximate an infinite continued fraction is to truncate the expansion after a given number of terms. Such a truncation -- a so-called k-term finite continued fraction -- has the form

Suppose that n and d are procedures of one argument (the term index i) that return the Ni and Di of the terms of the continued fraction. Define a procedure cont-frac such that evaluating (cont-frac n d k) computes the value of the k-term finite continued fraction. Check your procedure by approximating 1/ using

for successive values of k. How large must you make k in order to get an approximation that is accurate to 4 decimal places?

b. If your cont-frac procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.

Answer:

Exercise 1.38. In 1737, the Swiss mathematician Leonhard Euler published a memoir De Fractionibus Continuis, which included a continued fraction expansion for e - 2, where e is the base of the natural logarithms. In this fraction, the Ni are all 1, and the Di are successively 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, .... Write a program that uses your cont-frac procedure from exercise 1.37 to approximate e, based on Euler's expansion.

Answer:

Exercise 1.39. A continued fraction representation of the tangent function was published in 1770 by the German mathematician J.H. Lambert:

where x is in radians. Define a procedure (tan-cf x k) that computes an approximation to the tangent function based on Lambert's formula. K specifies the number of terms to compute, as in exercise 1.37.

Answer:

Exercise 1.40. Define a procedure cubic that can be used together with the newtons-method procedure in expressions of the form

to approximate zeros of the cubic x³ + ax² + bx + c.

Answer:

Exercise 1.41. Define a procedure double that takes a procedure of one argument as argument and returns a procedure that applies the original procedure twice. For example, if inc is a procedure that adds 1 to its argument, then (double inc) should be a procedure that adds 2. What value is returned by

Answer:

Double is a function that takes an input function and returns another function which applies the input twice. Therefore (double double) returns a function that applies its input 4 times. (double (double double)) therefore leads to a function that applies its input 4 * 4, or 16 times. Applying inc 16 times to 5 yields 21.

Exercise 1.42. Let f and g be two one-argument functions. The composition f after g is defined to be the function x f(g(x)). Define a procedure compose that implements composition. For example, if inc is a procedure that adds 1 to its argument,

Answer:

Exercise 1.43. If f is a numerical function and n is a positive integer, then we can form the nth repeated application of f, which is defined to be the function whose value at x is f(f(...(f(x))...)). For example, if f is the function x x + 1, then the nth repeated application of f is the function x x + n. If f is the operation of squaring a number, then the nth repeated application of f is the function that raises its argument to the 2nth power. Write a procedure that takes as inputs a procedure that computes f and a positive integer n and returns the procedure that computes the nth repeated application of f. Your procedure should be able to be used as follows:

Hint: You may find it convenient to use compose from exercise 1.42.

Answer:

Exercise 1.44. The idea of smoothing a function is an important concept in signal processing. If f is a function and dx is some small number, then the smoothed version of f is the function whose value at a point x is the average of f(x - dx), f(x), and f(x + dx). Write a procedure smooth that takes as input a procedure that computes f and returns a procedure that computes the smoothed f. It is sometimes valuable to repeatedly smooth a function (that is, smooth the smoothed function, and so on) to obtained the n-fold smoothed function. Show how to generate the n-fold smoothed function of any given function using smooth and repeated from exercise 1.43.

Exercise 1.46. Several of the numerical methods described in this chapter are instances of an extremely general computational strategy known as iterative improvement. Iterative improvement says that, to compute something, we start with an initial guess for the answer, test if the guess is good enough, and otherwise improve the guess and continue the process using the improved guess as the new guess. Write a procedure iterative-improve that takes two procedures as arguments: a method for telling whether a guess is good enough and a method for improving a guess. Iterative-improve should return as its value a procedure that takes a guess as argument and keeps improving the guess until it is good enough. Rewrite the sqrt procedure of section 1.1.7 and the fixed-point procedure of section 1.3.3 in terms of iterative-improve.

Answer:

Monday, December 22, 2008

SICP Section 1.2 Procedures and the Processes They Generate

Exercise 1.9. Each of the following two procedures defines a method for adding two positive integers in terms of the procedures inc, which increments its argument by 1, and dec, which decrements its argument by 1.

Using the substitution model, illustrate the process generated by each procedure in evaluating (+ 4 5). Are these processes iterative or recursive?

Answer: First version is recursive; second is iterative. Exercise 1.10. The following procedure computes a mathematical function called Ackermann's function.

What are the values of the following expressions?

Consider the following procedures, where A is the procedure defined above:

Give concise mathematical definitions for the functions computed by the procedures f, g, and h for positive integer values of n. For example, (k n) computes 5n2.

Answer:

Exercise 1.11. A function f is defined by the rule that f(n) = n if n<3 and f(n) = f(n - 1) + 2f(n - 2) + 3f(n - 3) if n> 3. Write a procedure that computes f by means of a recursive process. Write a procedure that computes f by means of an iterative process.

Exercise 1.12. The following pattern of numbers is called Pascal's triangle.

The numbers at the edge of the triangle are all 1, and each number inside the triangle is the sum of the two numbers above it.35 Write a procedure that computes elements of Pascal's triangle by means of a recursive process.

Answer:

Exercise 1.14. Draw the tree illustrating the process generated by the count-change procedure of section 1.2.2 in making change for 11 cents. What are the orders of growth of the space and number of steps used by this process as the amount to be changed increases?

Answer: Amount (steps and space) are respectively 1 (10), 2 (12), 3 (14) etc. Therefore space and # of steps grows linearly with amount. O(n).

Saturday, December 13, 2008

SICP section 1.1 The Elements of Programming

Exercise 1.1. Below is a sequence of expressions. What is the result printed by the interpreter in response to each expression? Assume that the sequence is to be evaluated in the order in which it is presented.

Exercise 1.2. Translate the following expression into prefix form

Exercise 1.3. Define a procedure that takes three numbers as arguments and returns the sum of the squares of the two larger numbers.
Exercise 1.4. Observe that our model of evaluation allows for combinations whose operators are compound expressions. Use this observation to describe the behavior of the following procedure:
Answer: The procedure a_plus_abs_b takes two arguments, a and b. It evaluates the expression (operator a b) where operator is chosen as either + or - depending on whether b is greater than zero or not. The key is that operator itself is the value of evaluating the if expression.

Exercise 1.5. Ben Bitdiddle has invented a test to determine whether the interpreter he is faced with is using applicative-order evaluation or normal-order evaluation. He defines the following two procedures:
Then he evaluates the expression
What behavior will Ben observe with an interpreter that uses applicative-order evaluation? What behavior will he observe with an interpreter that uses normal-order evaluation? Explain your answer. (Assume that the evaluation rule for the special form if is the same whether the interpreter is using normal or applicative order: The predicate expression is evaluated first, and the result determines whether to evaluate the consequent or the alternative expression.)

Answer: If applicative order is used for evaluation the arguments to test are evaluated first. This means (p) is evaluated, leading to an infinite loop. On the other hand with normal order evaluation (p) is not evaluated until it is actually needed. Since the if is designed in such a way that this never happens, there is no infinite loop and the call returns 0.

Exercise 1.6. Alyssa P. Hacker doesn't see why if needs to be provided as a special form. ``Why can't I just define it as an ordinary procedure in terms of cond?'' she asks. Alyssa's friend Eva Lu Ator claims this can indeed be done, and she defines a new version of if:
Eva demonstrates the program for Alyssa:
Delighted, Alyssa uses new-if to rewrite the square-root program:
What happens when Alyssa attempts to use this to compute square roots? Explain.

Answer: Normally if evaluates the alternative only if the predicate is false. This is why it is a special form. Since Alyssa's version is not a special form the alternative is evaluated irrespective of the result of the predicate. In the case of square roots this means calling sqrt-iter again, leading to an infinite loop.

SICP: Solutions to Exercises and Notes

I started my sabbatical in early July 2008 with the aim of working through the Structure and Interpretation of Computer Programs, exercises and all. I have completed the first three chapters at the time of writing this. So far I have been posting notes at the end of each chapter. I'll now start putting up my solutions to the exercises and any notes/questions I have.

All the exercises have been written in MzScheme using DrScheme. DrScheme's implementation of MzScheme worked straight out of the box for most purposes. The only serious tweaking I had to do so far was to add a macro for the cons-stream operation required in chapter 3. The code for this macro was borrowed from the PLT Scheme mailing list.

Thursday, December 11, 2008

Testing Code Highlighting Redux

I have been playing around with adding syntax highlighting for Scheme using syntaxhighlighter (albeit an old version of the tool). Here is a little test to see if it worked.

Sabbatical Update #3

I completed Chapter 3 of SICP today. It took longer than expected but was worth the effort I put in.

Chapter 3 started off by introducing state variables. This was quite new for chapters 1 and 2 used stateless procedures to solve problems. With the introduction of state came new problems. The substitution model of evaluation was no longer adequate to figure out how a given procedure would work. The authors introduced what is called the Environment Model as a better suited means of evaluation. The new model made good use of environment diagrams to help the process. In fact many exercise problems require the student to come up with environment diagrams along with the actual procedures.

The authors then focused on a prominent outcome of using assignment - mutable data. This involved learning to work with mutable lists and designing implementations of queues and tables. The understanding of mutable data and data structures were put to use in solving problems related to simulating digital circuits and constraint propagation.

The next section demonstrated the problems created when assignment and concurrency collide. Serialization was discussed in some depth as one possible way to control problems related to concurrency. I learned to implement simple mutexes and serializers.

The last section of the chapter - Streams - proved to be the most interesting and conceptually difficult to understand. In general streams are data structures used to represent sequences. They are distinct from lists in that they make use of delayed evaluation. What makes them fascinating is how such a powerful concept is built using such simple ingredients as force and delay.

Streams proved to be difficult to tackle in the beginning. The breakthrough came when I learned to ignore the syntax (the force and delay bits in particular) and look at streams purely as sequences, sometimes mathematical ones. Understanding stream operations became easier once I visualized these operations as "machinery working on moving assembly lines".

Wednesday, November 26, 2008

Comic Books and Graphic Novels

During a recent conversation a friend asked me about the difference between a 'Comic Book' and a 'Graphic Novel'. This was not the first time I had heard the question. Usually people wanted to know what I mean by 'graphic novel'. One gentleman wanted to know if I was using the phrase graphic novel to cover up the fact that I read comic books.

I'll take the second question first. I was surprised that someone would consider an adult reading comic books as unusual (unbecoming?). Perhaps I shouldn't have been so surprised given that I was talking to someone in the software industry, but I digress. In any case I was not trying to "cover up" my reading tastes by using the phrase. I buy and read graphic novels and comics openly; I don't hide my copies of Watchmen, V for Vendetta or Asterix, to name a few. I rank some of them among the best books I have read.

Why then distinguish between comic books and graphic novels? In my mind the distinction is not so much between children's and adults' reading but between the content and presentation. Take for example the 2005 movie Batman Begins. Contrast it with the 1985 vintage Batman. Both are based on the same comic book superhero and narrate similar stories. In spite of their similarities they both are significantly different products. The former is the movie equivalent of a graphic novel while the latter is firmly rooted in the comic book tradition. 'Begins' gained a far wider audience for the reason that it was a very enjoyable movie that happened to be based on a superhero. 'Batman' on the other hand was a movie that played mostly to the crowd already familiar with the story and were in the theater to watch a film adaptation.

The distinction is arguably subjective. I will list below the factors I use to differentiate a comic book from a graphic novel.

Non-traditional characters. Where traditional comic books have mostly focused on superheroes (with or without superpowers) graphic novels have told the stories of such mold-breaking characters like the Swamp Thing and John Constantine.
Different treatment of existing characters. This is most vividly illustrated by the success of recent movies like The Dark Knight. These movies were inspired by various graphic novels which told vastly new tales featuring familiar characters, sometimes casting them in an entirely new light.
Shorter, non-serial story arcs. Comic books typically use recurring characters and story lines that extend across lengthy arcs. Graphic novels are closer to traditional novels in that their story arcs are shorter. Classic examples include Alan Moore's V for Vendetta and Watchmen. This is not always true though; Neil Gaiman's Sandman spans multiple episodes, as do graphic novels featuring Batman.
Non-uniform presentation. Traditional comic books tend to have a relatively uniform look even when created by different artists. Graphic novels are known for using different artists with pronouncedly different styles in the same volume. The Sandman series is a good example.
Stylized depiction. This is related to the point mentioned above. Many Graphic novels use fantastically stylized depictions of characters. Frank Miller's Dark Knight, Sin City and 300 come to mind.
Reading experience comparable to traditional novels. This is quite subjective. I find the experience of reading graphic novels more comparable to reading traditional literature. Take for instance the character Death from Neil Gaiman's Sandman universe. I found that the two spin-off volumes featuring Death read like engrossing short stories.

Monday, October 27, 2008

SICP: Thinking Aloud

I am presently working on the third chapter of SICP. I found the opening section about environments and maintaining local state particularly interesting. After working through the exercises for the first two sections I started paraphrasing the authors' explanations in my mind to see if I had really understood the concepts. Most ideas were non-trivial but became malleable once I put in enough effort. However one particular exercise threw up questions that I could not clearly answer.

Here is some context to start with.

I know of two ways to define a procedure, say to square a given number, given below:

    ;; Form #1
    (define (square x) (* x x))

    ;; Form #2
    (define square (lambda (x) (* x x)))

Neither definition maintains state and both yield identical results for identical inputs. So far so good. Now consider the following procedure definition.

    (define f
      (let ((state 1))
        (lambda (x) (set! state (* state x)) state)))

    (+ (f 0) (f 1)) ;; returns 0
    
    ;; Reset interpreter and run with order of arguments to + reversed
    (+ (f 1) (f 0)) ;; returns 1

This procedure is easily explained. It maintains a local state variable initialized to 1. Inputs to the procedure are multiplied by the state, the existing state variable is replaced by the product and the new value of the state variable is returned. Consequently if the input to the procedure is ever 0 then the procedure will return 0 for all subsequent inputs. The state is not in the global environment but a local environment "attached" to the procedure. This local environment is easier to visualize when the let construct is replaced with an equivalent lambda expression.

    (define f
        ((lambda (state) (lambda (x) (set! state (* state x)) state)) 1))

My problems began when I tried to convert this definition to the "regular" form, i.e. (define (f x) ...). I tried the following, with and without the let construct:

    (define (f x)
      (let ((state 1))
        (set! state (* state x))
        state))

I was not sure if this would work; evaluating the test expressions quickly confirmed my suspicions. The two definitions were NOT equivalent. Unlike the first form the "regular" form did not seem to maintain state across invocations. Here is my understanding of what is happening.

When the procedure body is evaluated the value of state is set to 1 in the corresponding frame. The state is indeed changed to the product using the set! call. However nothing is changed in the "nearest" environment, which is the global environment. The frame is discarded when the procedure terminates and the state is lost. In the earlier case the attached local environment stayed alive even after the procedure terminated thereby enabling it to preserve state.

To test my theory I moved the state variable to the global environment. Everything worked as expected thereafter.

    (define state 1)

    (define (f x)
      (set! state (* state x))
      state)

My explanation notwithstanding, two questions remain.

Is my understanding correct?
Is it possible to convert the procedure from one form to another without resorting to defining state globally? If so, how?

I hope that my questions will be automatically answered as I learn more. In the meantime please let me know if you have any thoughts on the topic.

PS: Thanks to Magicindian for helping me to derive my questions from what started out as a vague tangent of the solution to an SICP exercise. He has a particular talent for distilling clear and concise ideas from tangled masses of thoughts. He gave me several useful inputs which I neglected to write down. I promise to keep notes the next time I have interesting discussions with my friends and report them along with the final summary.

Thursday, September 25, 2008

Sabbatical Update #2

I completed Chapter 2 of SICP yesterday. I am taking the day off from my regularly scheduled activities to rest and recuperate and also to write this mini-report.

While chapter 1 was definitely interesting the second chapter was far more meatier in terms of fundamental concepts presented and explored. I have written code mostly in Python and Java and had very conventional notions of 'data' in the programming context. The authors of SICP challenge that notion almost right from the beginning of the chapter. They present - and illustrate - the idea that data can be thought of as "some collection of selectors and constructors, together with specified conditions that these procedures must fulfill in order to be a valid representation". The rest of the chapter builds on this fundamental concept working on more complex data including a mini "picture language".

It took me some time to digest this idea and longer to deal with some of the exercises. One particular exercise involved implementing Church Numerals using Scheme. Church Numerals are the brain child of mathematician Alonzo Church who first described a way to embed data and operators into lambda calculus. I thought the name 'Church Numerals' was a misnomer seeing that these were not 'numerals' in any way I have come to understand :-P Jokes aside the exercise was thought provoking. In case you were wondering this is what "0" and "1" look like:

    ;; zero
    (define zero (lambda (f) (lambda (x) x)))

    ;; one
    (define one (lambda (f) (lambda (x) (f x))))

I later realized that my troubles arose from my focus on the form of numbers rather than the function they served. Once I understood the distinction between the two it became easier to address the problem.

On a related note I will be putting up my solutions to the SICP problems shortly, starting with Chapter 2.

Wednesday, August 13, 2008

Another Recital and Related Thoughts

I played the Piano at a small recital organised in my teacher's home last month. This was my second recital this year. I played two pieces - Theme and Variations by Theodore Kullak and Rocking Horse Ride (Opus 98, No. 5) by Alexander Gretchaninov. Kullak's piece presents a theme followed by five variations of that theme. The hand positions are fixed and the tempo increases in the fourth and fifth variations. 'Rocking Horse Ride' is taken from Gretchaninov's 'Children's Book'. It tells about a rocking horse that starts off slowly enough but soon accelerates and almost rocks too far. But all is well in the end.

The single most important difference from my previous recital was my increased confidence. This was not entirely surprising given that I had prepared myself better this time around. It helped that I had been out of work for a couple of weeks before D-Day. And I forced myself to take a quick nap in the afternoon before the event. It was a refreshing contrast from the previous before-recital afternoon when I was tightly wound up and excited.

All of it paid off in the end. I did not mess up any notes but I did feel that I could have done better on the dynamics.

On a related note I was told that my music practice had noticeably improved ever since I left my job. This was a bit surprising especially since I had not drastically lengthened my practice sessions. I think reduced stress levels made most of the difference. In retrospect I can see that work had been so draining that I had become used to being perpetually wound up and did not notice how it was degrading the quality of my life.

I don't seem to be the alone in being stressed out. I learned from my teacher that there was a time when recitals were far more frequent. According to her pupils these days (that includes me) take much longer to get ready for a recital. She stressed how barely half a generation ago pupils - who were also at school, had a job or were otherwise busy - were somehow able to find time to do justice to music. With every passing year pupils seem to have less and less time to practice, or indeed to focus on anything much outside work.

I have decided to actively combat stress the next time I start working a job. This would mean working regular hours, leaving work behind on stepping out of the office, learning to turn off my phone after hours and during weekends. I don't know how I'll achieve all these but I certainly am not going to let work deprive me of life again.

Sunday, August 10, 2008

State of the Sabbatical

Yesterday marked the end of the first month of my sabbatical. I used the opportunity to sit back and take stock of how far I have progressed towards achieving my goals. For the record I started on my sabbatical aiming to achieve the following before November:

Work through Structure and Interpretation of Computer Programs (SICP), exercises and all
Learn to play Muzio Clementi's Sonatina in C Major (Opus 36 No. 1) well enough to give a recital
Read one (non fiction) book every fortnight

Here follows then a quick summary of the state of the sabbatical.

At the time of writing this I have completed the first of five chapters of SICP and started on the second. I am presently working on the second of three movements of the Sonatina. I finished reading 'The Audacity of Hope' and am looking for another book.

Working through SICP is proving to be an eye opener. The exercises look deceptively simple until you try to work them out. I was *very* frustrated in the beginning but am learning relax and re-focus. Some of the ideas took a while to wrap my mind around due to various factors. I had never worked in Scheme before and found it difficult to write programs without explicit looping constructs and variable assignment. For this reason the Chapter 1 exercises dealing with converting recursive procedures to iterative and vice-versa troubled me for several days. I was shocked to notice how long it took me to understand and digest fundamental concepts like lambda. Easy work in enterprise software for 8 plus years seems to have damaged most of my gray cells :(

The Sonatina is proving tough to crack. The first movement was relatively simple. But then came the second movement with its triplets, trills and one-sixteenth notes. It quickly deprived me of the warm glow of working through the first. So far I have hammed my way through five lines. The last line is adamantly refusing to submit.

'The Audacity of Hope' is a very engrossing read. It is rare to see a politician writing for himself without relying on ghost writers. It was evident after reading the book that Senator Obama can not only write for himself but matches his words with sharp thought and keen observations.

That is all in this week's report. More soon.

Wednesday, April 23, 2008

Stuck in a Time Frame

The topic of some mutual friends came up during a recent conversation I had with a friend. After I filled her in about their whereabouts and activities she remarked that said friends and yours truly were "stuck in a time frame". I understood what she meant in the context of our conversation. I realised that she had merely expressed in a catchy phrase an opinion others had expressed before using different words. In order to fully understand the import of 'stuck in a time frame' I will first try to illustrate its opposite concept. 'Moving through time frames', if you will.

The basis of my explanation is my understanding that the (suburban, educated) Indian society expects individuals to live their life in a certain way based on their age "time frame". In Kerala the teen years are considered to be the time for education. You are expected to be in college by your late teens. Some of the non-curricular pursuits of a typical student include dabbling in new hobbies and other activities. These are mostly but not always tolerated. For instance I picked up Miniature Wargaming as a hobby in college. I hasten to add that individuals are expected to outgrow their hobbies or interests as they move on to the next stage in life.

For my generation a person's twenties is the time for seeking gainful employment, sometimes after completing higher studies. As travelling overseas became more common and affordable people were expected to switch to "explore" mode after landing a job. Non-curricular activities of this time frame include visiting various places, picking up hobbies that are made more affordable by technology etc. Most notable among the latter is Photography. Of course there are people I know who used to save their allowances to make money for Photography while in college but that is another story.

Mid to late twenties, as I was told by more than one person, is the time to move on again. Marriage is *the* key social event marking the end of this time frame. This is such a strong social expectation that unmarried people are treated almost as if they are in mortal danger and pose a threat to others. It is common for bachelors and spinsters to be asked even by virtual strangers why they haven't married. Marriage itself is the outcome of a filtration process demanded by society and community and initiated by parents. Criteria of filtration include religion, caste, community, state, and language to mention a few. A list of desirables passing the filter conditions is presented to the "end user" and he or she can pick any one. There indeed are exceptions but these remain a very small minority.

A man in his thirties is expected to start a family and "engage society more actively". "Engaging society" means, among other things, actively participating in social events that you were given permission to avoid as a twenty-something. Hobbies are frowned upon unless they are strictly mainstream. Non work related pursuits are allowed as long as they are for buying a new car, apartment or real estate.

I don't know quite clearly what my generation is expected to do in our forties, fifties and subsequent decades. I speculate that our forties would be the time to focus on children and career growth punctuated by the occasional mid life crisis. The fifties would be time to coordinate marriages of children born to the Indian software generation.

It is interesting to note how a bit of this progression is reflected in the photo galleries of a social networking site popular with Indians. First, snaps of the protagonist in various places around the globe. Some capture their first car or apartment. Marriage photos and pictures of the sweetheart appear some time later. These are in turn replaced by pictures of children and group photographs.

Coming back to my conversation I found that my friend's opinion was apparently based on her observations of the individuals' lives. None of the people we discussed including yours truly had "moved on" as she expected. At least two in the list are pursuing higher studies in their thirties, that too in subjects not necessarily related to their present careers. Three are not married and don't plan to. Not to mention their hobbies. I counted several different hobbies in the group ranging from dancing to miniature wargaming to semi-professional poker to playing the Mridangam.

I told my friend that all the people we discussed had merely chosen to define the (time) segments making up their life differently. I was not convinced by her arguments that one should drastically change his outlook on life for the sole purpose of meeting popular definitions of "moving on". As far as I see each one of these people *have* been moving on. They are more skilled, know more about their favourite subjects now than they did five years ago and are by no means staying still in any of their chosen fields of endeavour. If anything almost all of them rue that they are not moving forward as fast as they would like to.

Friday, April 18, 2008

A Tale of Two Movies

The acclaimed Malayalam movie 'Paithrikam' came out in 1993, the year I finished school. Directed by Jayaraj the movie told the story of two generations of a Kerala Brahmin family. The father is a soft spoken orthodox Brahmin well respected in the community and a learned scholar-performer of rituals and Yajnas. His eldest son is a vocal atheist who is openly against theism in all its forms including his family's rituals and cloistered lifestyle. Caught between the two are a loving younger brother and a largely silent mother. The movie builds towards a confrontation between the beliefs of father and son culminating in a final act where the son undergoes a spiritual conversion and takes his father's place.

The movie is commendable on its own merits. However I remember it for different reasons. As a Brahmin I witnessed first hand how 'Paithrikam' became quite popular in the Brahmin community shortly after its release. For a while after the movie came out its name came up during conversations in many families including mine. Relatives had good things to say about the movie at family gatherings. I distinctly recall seeing advertisements for the movie endorsed by prominent Brahmin priests and scholars. These usually said something like "I strongly recommend everyone to watch it" or "a poignant narrative". I believe that for some people the movie came as an affirmation of their strongly held beliefs about the "superiority" of Brahmin culture and tradition. Some perceived the movie to be in agreement with their reservations against atheism and progressive trends in the community.

I will not discuss the merits of such beliefs but instead skip ahead to narrate the tale of another movie that came out barely a year later. Hariharan's 'Parinayam', scripted by veteran Malayalam writer M.T. Vasudevan Nair also centred on a Brahmin family. The movie was set in the turbulent decades of late 19th and early 20th centuries that witnessed several changes in India's social order. The events portrayed in the movie occur not long after the Kerala Brahmin community was scandalised by the ritual trial of a Brahmin widow Savithri, alias Thathrikkutty, for adultery. The accused named no less than sixty four prominent persons from different castes as her lovers. This was also the time when progressives led by reformers like V.T. Bhattathirippad organised a movement against social ills prevalent in the Brahmin community.

'Parinayam' is the story of a young Brahmin girl who becomes the fourth wife, and widow shortly thereafter, of an old Brahmin lord. She becomes pregnant after her husband's death and is tried by a communal tribunal. The movie ends with her being cast out from home and community and starting an independent, defiant life with the help of her rebel/reformer stepson.

Here again the movie shines and can be enjoyed for its own merits. What I want to point out however is how this movie was hardly ever mentioned by the same people who were all praise for the earlier one. Going strictly by quantity and extent of Brahmin traditions portrayed the second movie should have attracted a much wider audience. And yet it failed to be even so much as mentioned in gatherings, much less admired.

Why this difference? I thought about this after I watched 'Parinayam' again very recently. I think that many in the Kerala Brahmin community are guilty of selective adoption and propagation of events defining its History. The dark tales are entirely left out when the story of a vibrant socio-religious past is told. Consequently many youngsters grow up with a skewed knowledge of history which only serves to enforce their illogical belief in superiority by virtue of birth in an "upper" caste.

In this context it is interesting to inspect how the community organisation formed by Bhattathirippad to combat social ills has evolved. What once was the refuge of rebels and progressives is now the gathering place for conservatives and the orthodox. Where membership was once a statement of rebellion today it is a bellwether of social prominence.

I have a firmly held belief that a person's caste has nothing to do with how good or bad a person he is. My beliefs aside I still wish that those who give importance to belonging to a community were more objective in drawing lessons from its past. For it is a fact of history that for every 'Paithrikam' there are all too many 'Parinayam's.

Mentioned In Dispatches

Wednesday, January 07, 2009

SICP Section 2.2 Hierarchical Data and the Closure Property - Part 1

Saturday, December 27, 2008

SICP Section 2.1 Introduction to Data Abstraction

Tuesday, December 23, 2008

SICP Section 1.3 Formulating Abstractions with Higher-Order Procedures

Monday, December 22, 2008

SICP Section 1.2 Procedures and the Processes They Generate

Saturday, December 13, 2008

SICP section 1.1 The Elements of Programming

SICP: Solutions to Exercises and Notes

Thursday, December 11, 2008

Testing Code Highlighting Redux

Sabbatical Update #3

Wednesday, November 26, 2008

Comic Books and Graphic Novels

Monday, October 27, 2008

SICP: Thinking Aloud

Thursday, September 25, 2008

Sabbatical Update #2

Wednesday, August 13, 2008

Another Recital and Related Thoughts

Sunday, August 10, 2008

State of the Sabbatical

Wednesday, April 23, 2008

Stuck in a Time Frame

Friday, April 18, 2008

A Tale of Two Movies

egmanoj@twitter

Blog Archive

Labels

Read Also

About Me

Wednesday, January 07, 2009

Saturday, December 27, 2008

Tuesday, December 23, 2008

Monday, December 22, 2008

Saturday, December 13, 2008

Thursday, December 11, 2008

Wednesday, November 26, 2008

Monday, October 27, 2008

Thursday, September 25, 2008

Wednesday, August 13, 2008

Sunday, August 10, 2008

Wednesday, April 23, 2008

Friday, April 18, 2008

egmanoj@twitter

Blog Archive

Labels

Subscribe

Read Also

About Me