SICP Section 2.1 Introduction to Data Abstraction

Exercise 2.1. Define a better version of make-rat that handles both positive and negative arguments. Make-rat should normalize the sign so that if the rational number is positive, both the numerator and denominator are positive, and if the rational number is negative, only the numerator is negative.

Answer:
(define (make-rat n d) (let ((g (gcd n d)) (ratio (/ n d))) (if (> ratio 0.0) (cons (/ n g) (/ d g)) (cons (- (abs (/ n g))) (abs (/ d g))))))
Exercise 2.2. Consider the problem of representing line segments in a plane. Each segment is represented as a pair of points: a starting point and an ending point. Define a constructor make-segment and selectors start-segment and end-segment that define the representation of segments in terms of points. Furthermore, a point can be represented as a pair of numbers: the x coordinate and the y coordinate. Accordingly, specify a constructor make-point and selectors x-point and y-point that define this representation. Finally, using your selectors and constructors, define a procedure midpoint-segment that takes a line segment as argument and returns its midpoint (the point whose coordinates are the average of the coordinates of the endpoints). To try your procedures, you'll need a way to print points:
(define (print-point p) (newline) (display "(") (display (x-point p)) (display ",") (display (y-point p)) (display ")"))
Answer:
;; Point (define (make-point x y) (cons x y)) (define (x-point p) (car p)) (define (y-point p) (cdr p)) ;; Line segment (define (make-segment start end) (cons start end)) (define (start-segment seg) (car seg)) (define (end-segment seg) (cdr seg)) (define (print-point p) (display "(") (display (x-point p)) (display ",") (display (y-point p)) (display ")")) (define (midpoint-segment seg) (let ((start (start-segment seg)) (end (end-segment seg))) (let ((x1 (x-point start)) (y1 (y-point start)) (x2 (x-point end)) (y2 (y-point end))) (make-point (average x1 x2) (average y1 y2))))) ;; (define seg (make-segment (make-point 0 1) (make-point 2 1))) ;; (print-point (midpoint-segment seg)) ;; (1,1)
Exercise 2.3. Implement a representation for rectangles in a plane. (Hint: You may want to make use of exercise 2.2.) In terms of your constructors and selectors, create procedures that compute the perimeter and the area of a given rectangle. Now implement a different representation for rectangles. Can you design your system with suitable abstraction barriers, so that the same perimeter and area procedures will work using either representation?

Answer:
(define (make-rect p1 p2 p3 p4) (cons (cons p1 p2) (cons p3 p4))) (define (length-seg seg) (let ((start (start-segment seg)) (end (end-segment seg))) (let ((x1 (x-point start)) (y1 (y-point start)) (x2 (x-point end)) (y2 (y-point end))) (sqrt (+ (square (- x2 x1)) (square (- y2 y1))))))) (define (rect-length r) (let ((p1 (car (car r))) (p2 (cdr (car r)))) (let ((side (make-segment p1 p2))) (length-seg side)))) (define (rect-breadth r) (let ((p1 (car (car r))) (p4 (cdr (cdr r)))) (let ((side (make-segment p1 p4))) (length-seg side)))) (define (perimeter r) (* 2 (+ (rect-length r) (rect-breadth r)))) (define (area r) (* (rect-length r) (rect-breadth r))) ;; (define r (make-rect ;; (make-point 0 0) ;; (make-point 0 1) ;; (make-point 2 1) ;; (make-point 2 0))) ;; (perimeter r) ;; 6 ;; (area r) ;; 2
Exercise 2.4. Here is an alternative procedural representation of pairs. For this representation, verify that (car (cons x y)) yields x for any objects x and y.
(define (cons x y) (lambda (m) (m x y))) (define (car z) (z (lambda (p q) p)))
What is the corresponding definition of cdr? (Hint: To verify that this works, make use of the substitution model of section 1.1.5.)

Answer:
(define (cons1 x y) (lambda (m) (m x y))) (define (car1 z) (z (lambda (p q) p))) ;; cdr (define (cdr1 z) (z (lambda (p q) q))) ;; (car1 (cons1 2 1)) ;; 2 ;; (cdr1 (cons1 2 1)) ;; 1
Exercise 2.5. Show that we can represent pairs of nonnegative integers using only numbers and arithmetic operations if we represent the pair a and b as the integer that is the product 2a 3b. Give the corresponding definitions of the procedures cons, car, and cdr.

Answer:
(define (count-powers-of-n number n) (define (iter count number) (if (and (= (remainder number n) 0) (>= number n)) (iter (+ 1 count) (/ number n)) count)) (iter 0 number)) (define (count-powers-of-2 number) (count-powers-of-n number 2)) (define (count-powers-of-3 number) (count-powers-of-n number 3)) (define (n-cons a b) (* (expt 2 a) (expt 3 b))) (define (n-car z) (count-powers-of-2 z)) (define (n-cdr z) (count-powers-of-3 z)) ;; (n-car (n-cons 10 11)) ;; 10 ;; (n-cdr (n-cons 10 11)) ;; 11
Exercise 2.6. In case representing pairs as procedures wasn't mind-boggling enough, consider that, in a language that can manipulate procedures, we can get by without numbers (at least insofar as nonnegative integers are concerned) by implementing 0 and the operation of adding 1 as
(define zero (lambda (f) (lambda (x) x))) (define (add-1 n) (lambda (f) (lambda (x) (f ((n f) x)))))
This representation is known as Church numerals, after its inventor, Alonzo Church, the logician who invented the calculus.

Define one and two directly (not in terms of zero and add-1). (Hint: Use substitution to evaluate (add-1 zero)). Give a direct definition of the addition procedure + (not in terms of repeated application of add-1).

Answer:
(define zero (lambda (f) (lambda (x) x))) (define (add-1 n) (lambda (f) (lambda (x) (f ((n f) x))))) ;; one (define one (lambda (f) (lambda (x) (f x)))) ;; two (define two (lambda (f) (lambda (x) (f (f x))))) ;; + (define (church+ m n) (lambda (f) (lambda (x) ((m f) ((n f) x)))))
Exercise 2.7. Alyssa's program is incomplete because she has not specified the implementation of the interval abstraction. Here is a definition of the interval constructor:
(define (make-interval a b) (cons a b))
Define selectors upper-bound and lower-bound to complete the implementation.

Answer:
;; selectors (define (lower-bound interval) (car interval)) (define (upper-bound interval) (cdr interval))
Exercise 2.8. Using reasoning analogous to Alyssa's, describe how the difference of two intervals may be computed. Define a corresponding subtraction procedure, called sub-interval.

Answer:
(define (sub-interval x y) (make-interval (- (lower-bound x) (upper-bound y)) (- (upper-bound x) (lower-bound y))))
Exercise 2.10. Ben Bitdiddle, an expert systems programmer, looks over Alyssa's shoulder and comments that it is not clear what it means to divide by an interval that spans zero. Modify Alyssa's code to check for this condition and to signal an error if it occurs.


(define (spans-zero? interval) (and (< (lower-bound interval) 0) (> (upper-bound interval) 0))) (define (div-interval x y) (if (spans-zero? y) (error "Denominator interval spans zero" y) (mul-interval x (make-interval (/ 1.0 (upper-bound y)) (/ 1.0 (lower-bound y))))))
Exercise 2.11. In passing, Ben also cryptically comments: ``By testing the signs of the endpoints of the intervals, it is possible to break mul-interval into nine cases, only one of which requires more than two multiplications.'' Rewrite this procedure using Ben's suggestion.

After debugging her program, Alyssa shows it to a potential user, who complains that her program solves the wrong problem. He wants a program that can deal with numbers represented as a center value and an additive tolerance; for example, he wants to work with intervals such as 3.5± 0.15 rather than [3.35, 3.65]. Alyssa returns to her desk and fixes this problem by supplying an alternate constructor and alternate selectors:
(define (make-center-width c w) (make-interval (- c w) (+ c w))) (define (center i) (/ (+ (lower-bound i) (upper-bound i)) 2)) (define (width i) (/ (- (upper-bound i) (lower-bound i)) 2))
Unfortunately, most of Alyssa's users are engineers. Real engineering situations usually involve measurements with only a small uncertainty, measured as the ratio of the width of the interval to the midpoint of the interval. Engineers usually specify percentage tolerances on the parameters of devices, as in the resistor specifications given earlier.

Answer:
(define (above-zero? interval) (and (> (lower-bound interval) 0) (> (upper-bound interval) 0))) (define (below-zero? interval) (and (< (lower-bound interval) 0) (< (upper-bound interval) 0))) (define (mul-interval x y) (let ((l1l2 (* (lower-bound x) (lower-bound y))) (l1u2 (* (lower-bound x) (upper-bound y))) (u1l2 (* (upper-bound x) (lower-bound y))) (u1u2 (* (upper-bound x) (upper-bound y)))) (cond ((and (above-zero? x) (above-zero? y)) (make-interval l1l2 u1u2)) ((and (above-zero? x) (spans-zero? y)) (make-interval u1l2 u1u2)) ((and (spans-zero? x) (above-zero? y)) (make-interval l1u2 u1u2)) ((and (above-zero? x) (below-zero? y)) (make-interval u1u2 l1l2)) ((and (below-zero? x) (above-zero? y)) (make-interval u1u2 l1l2)) ((and (below-zero? x) (spans-zero? y)) (make-interval l1u2 l1l2)) ((and (spans-zero? x) (below-zero? y)) (make-interval u1l2 l1l2)) ((and (below-zero? x) (below-zero? y)) (make-interval u1u2 l1l2)) ((and (spans-zero? x) (spans-zero? y)) (make-interval (min l1u2 u1l2) (min l1l2 u1u2))))))
Exercise 2.12. Define a constructor make-center-percent that takes a center and a percentage tolerance and produces the desired interval. You must also define a selector percent that produces the percentage tolerance for a given interval. The center selector is the same as the one shown above.

Answer:
(define (center i) (/ (+ (lower-bound i) (upper-bound i)) 2)) (define (make-center-percent c p) (let ((p-value (/ (* c p) 100))) (make-interval (- c p-value) (+ c p-value))))
Exercise 2.13. Show that under the assumption of small percentage tolerances there is a simple formula for the approximate percentage tolerance of the product of two intervals in terms of the tolerances of the factors. You may simplify the problem by assuming that all numbers are positive.

After considerable work, Alyssa P. Hacker delivers her finished system. Several years later, after she has forgotten all about it, she gets a frenzied call from an irate user, Lem E. Tweakit. It seems that Lem has noticed that the formula for parallel resistors can be written in two algebraically equivalent ways:

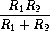
and

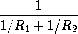
He has written the following two programs, each of which computes the parallel-resistors formula differently:
(define (par1 r1 r2) (div-interval (mul-interval r1 r2) (add-interval r1 r2))) (define (par2 r1 r2) (let ((one (make-interval 1 1))) (div-interval one (add-interval (div-interval one r1) (div-interval one r2)))))
Lem complains that Alyssa's program gives different answers for the two ways of computing. This is a serious complaint.

Answer: Let x and y be two intervals and dx and dy their respective tolerances. Their product can be calculated as (x + dx) * (y + dy). Expanding this we get xy + xdy + ydx + dxdy. As dx and dy are small to begin with their product will be very small and can be ignored without losing much accuracy. The equation then becomes xy + xdy + ydx.

If we call the product z, with a tolerance dz, then z + dz = xy + xdy + ydx. Separating z and dz, we get dz = xdy + ydx. This is the relation between the tolerance of the product the individual tolerances.

Exercise 2.14. Demonstrate that Lem is right. Investigate the behavior of the system on a variety of arithmetic expressions. Make some intervals A and B, and use them in computing the expressions A/A and A/B. You will get the most insight by using intervals whose width is a small percentage of the center value. Examine the results of the computation in center-percent form (see exercise 2.12).

Answer: Lem's hypothesis is easily proven right. Take the example below.
(define (par1 r1 r2) (div-interval (mul-interval r1 r2) (add-interval r1 r2))) (define (par2 r1 r2) (let ((one (make-interval 1 1))) (div-interval one (add-interval (div-interval one r1) (div-interval one r2))))) (define x (make-center-percent 3 0.1)) (define y (make-center-percent 7 0.1)) (par1 x y) ;; (2.0937083916083914 . 2.1063084084084083) (par2 x y) ;; (2.0979 . 2.1021)
The problem stems from the fact that the formulae do not take intervals into consideration whereas the code does. For instance the interval one implicitly assumes that R1/R1 = R2/R2 = 1. However this is only true when intervals are not involved. Hence the two formulae give two different results.

Exercise 2.15. Eva Lu Ator, another user, has also noticed the different intervals computed by different but algebraically equivalent expressions. She says that a formula to compute with intervals using Alyssa's system will produce tighter error bounds if it can be written in such a form that no variable that represents an uncertain number is repeated. Thus, she says, par2 is a ``better'' program for parallel resistances than par1. Is she right? Why?

Answer: Eva is correct. As we are operating with intervals rather than whole numbers it is better to reduce the "occurrence" of intervals in any given formula to a minimum. This reduces the number of ways in which errors can creep in and thereby produces tighter bounds. As the second formula has fewer occurrences of the intervals it will produce tighter bounds.

Exercise 2.16. Explain, in general, why equivalent algebraic expressions may lead to different answers. Can you devise an interval-arithmetic package that does not have this shortcoming, or is this task impossible? (Warning: This problem is very difficult.)

Answer: The answer is similar those of the two previous questions. The main reason is the difference between using whole numbers and intervals. Normal properties and rules of algebra that apply to whole numbers do not hold true when intervals are used. For instance, while x/x = 1 when x and y are non zero whole numbers this is not so for cases when x is an interval. Likewise x - x need not be zero and so on.

It *might* be possible to develop a package provided such concepts as inverse can be defined for an interval. I am not sure how to go about the definitions though.

SICP Section 1.3 Formulating Abstractions with Higher-Order Procedures

Exercise 1.29. Simpson's Rule is a more accurate method of numerical integration than the method illustrated above. Using Simpson's Rule, the integral of a function f between a and b is approximated as

where h = (b - a)/n, for some even integer n, and yk = f(a + kh). (Increasing n increases the accuracy of the approximation.) Define a procedure that takes as arguments f, a, b, and n and returns the value of the integral, computed using Simpson's Rule. Use your procedure to integrate cube between 0 and 1 (with n = 100 and n = 1000), and compare the results to those of the integral procedure shown above.

Answer:
(define (sum term a next b) (if (> a b) 0 (+ (term a) (sum term (next a) next b)))) (define (integral f a b dx) (define (add-dx x) (+ x dx)) (* (sum f (+ a (/ dx 2.0)) add-dx b) dx)) ;; solution (define (s-integral f a b n) (define h (/ (- b a) n)) (define (factor x) (cond ((or (= x 0) (= x n)) 1) ((= (modulo x 2) 0) 2) (else 4))) (define (s-term k) (define a-plus-kh (+ a (* k h))) (* (factor k) (f a-plus-kh))) (define (s-next x) (+ 1 x)) (* (/ h 3) (sum s-term a s-next n)))
Exercise 1.30. The sum procedure above generates a linear recursion. The procedure can be rewritten so that the sum is performed iteratively. Show how to do this by filling in the missing expressions in the following definition:
(define (sum term a next b) (define (iter a result) (if <??> <??> (iter <??> <??>))) (iter <??> <??>))
Answer:
(define (sum term a next b) (define (iter a result) (if (= a b) (+ result (term a)) (iter (next a) (+ result (term a))))) (iter a 0))
Exercise 1.31. a. The sum procedure is only the simplest of a vast number of similar abstractions that can be captured as higher-order procedures. Write an analogous procedure called product that returns the product of the values of a function at points over a given range. Show how to define factorial in terms of product. Also use product to compute approximations to using the formula
b. If your product procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.

Answer:
;; product similar to sum (define (product term a next b) (if (> a b) 1 (* (term a) (product term (next a) next b)))) ;; Factorial using product defined above. (define (identity x) x) (define (factorial-1 n) (product identity 1 inc n)) ;; Calculating pi using John Wallis' formula. (define (pi n) (define b (* 2 n)) (define (add2 x) (+ x 2)) (define (num-term x) (if (or (= x 2) (= x b)) x (square x))) (* 4.0 (/ (product num-term 2 add2 b) (product square 3 add2 (- b 1))))) ;; Product as iterative. (define (i-product term a next b) (define (iter a result) (if (= a b) (* result (term a)) (iter (next a) (* result (term a))))) (iter a 1))
Exercise 1.32. a. Show that sum and product (exercise 1.31) are both special cases of a still more general notion called accumulate that combines a collection of terms, using some general accumulation function:
(accumulate combiner null-value term a next b)
Accumulate takes as arguments the same term and range specifications as sum and product, together with a combiner procedure (of two arguments) that specifies how the current term is to be combined with the accumulation of the preceding terms and a null-value that specifies what base value to use when the terms run out. Write accumulate and show how sum and product can both be defined as simple calls to accumulate.
b. If your accumulate procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.

Answer
;; Accumulate (define (accumulate combiner null-value term a next b) (if (> a b) null-value (combiner (term a) (accumulate combiner null-value term (next a) next b)))) ;; sum and product defined using accumulate (define (a-sum term a next b) (accumulate + 0 term a next b)) (define (a-product term a next b) (accumulate * 1 term a next b)) ;; Iterative accumulate (define (i-accumulate combiner null-value term a next b) (define (iter a result) (if (= a b) (combiner result (term a)) (iter (next a) (combiner result (term a))))) (iter a null-value)) (define (i-sum term a next b) (i-accumulate + 0 term a next b)) (define (i-product term a next b) (i-accumulate * 1 term a next b))
Exercise 1.33. You can obtain an even more general version of accumulate (exercise 1.32) by introducing the notion of a filter on the terms to be combined. That is, combine only those terms derived from values in the range that satisfy a specified condition. The resulting filtered-accumulate abstraction takes the same arguments as accumulate, together with an additional predicate of one argument that specifies the filter. Write filtered-accumulate as a procedure. Show how to express the following using filtered-accumulate:

a. the sum of the squares of the prime numbers in the interval a to b (assuming that you have a prime? predicate already written)

b. the product of all the positive integers less than n that are relatively prime to n (i.e., all positive integers i < n such that GCD(i,n) = 1).

Answer:
(define (filtered-accumulate combiner filter null-value term a next b) (define (_combine result x) (if (filter x) (combiner result (term x)) result)) (define (iter a result) (if (= a b) (_combine result a) (iter (next a) (_combine result a)))) (iter a null-value)) (define (sum-even term a next b) (define (even? x) (= 0 (modulo x 2))) (filtered-accumulate + even? 0 term a next b))
Exercise 1.34. Suppose we define the procedure
(define (f g) (g 2))
Then we have
(f square) 4 (f (lambda (z) (* z (+ z 1)))) 6
What happens if we (perversely) ask the interpreter to evaluate the combination (f f)? Explain.

Answer: f is a procedure that accepts another procedure g as its argument. When executed f calls g, passing 2 as argument. In the first example the argument procedure is square. When square is called with 2 as its argument the result is naturally 4.

When we try to call f passing itself as an argument the following things happen:

1. The first time f receives a procedure, f, as its argument.
2. The argument is then invoked, passing 2 as a parameter. As the argument is f itself, this means invoking (f 2)
3. The argument to f now is 2, leading to (2 2) being invoked. This causes as the interpreter expects the first item in the expression to be a procedure but instead gets 2.

Exercise 1.35. Show that the golden ratio (section 1.2.2) is a fixed point of the transformation x 1 + 1/x, and use this fact to compute by means of the fixed-point procedure.

Answer:
(define tolerance 0.00001) (define (fixed-point f first-guess) (define (close-enough? v1 v2) (< (abs (- v1 v2)) tolerance)) (define (try guess count) (let ((next (f guess))) (if (close-enough? guess next) next (try next (+ count 1))))) (try first-guess 1)) ;; Calculating golden ratio phi ;; (fixed-point (lambda (x) (+ 1 (/ 1 x))) 1.0) ;; Requires 14 steps ;; = 1.6180327868852458 ;; (fixed-point (lambda (x) (average x (+ 1 (/ 1 x)))) 2.0) ;; Requires 10 steps ;; = 1.6180311591702674
Exercise 1.36. Modify fixed-point so that it prints the sequence of approximations it generates, using the newline and display primitives shown in exercise 1.22. Then find a solution to xx = 1000 by finding a fixed point of x log(1000)/log(x). (Use Scheme's primitive log procedure, which computes natural logarithms.) Compare the number of steps this takes with and without average damping. (Note that you cannot start fixed-point with a guess of 1, as this would cause division by log(1) = 0.)

Answer:
(define (fixed-point f first-guess) (define (close-enough? v1 v2) (< (abs (- v1 v2)) tolerance)) (define (try guess count) (let ((next (f guess))) (display count) (display ": ") (display guess) (newline) (if (close-enough? guess next) next (try next (+ count 1))))) (try first-guess 1)) ;; Calculating fp for x^x = 1000 without damping ;; Requires 34 steps ;; (fixed-point (lambda (x) (/ (log 1000) (log x))) 2.0) ;; = 4.555532270803653 ;; Calculating fp for x^x = 1000 with damping ;; Requires 9 steps ;; (fixed-point (lambda (x) (average x (/ (log 1000) (log x)))) 2.0) ;; = 4.555537551999825
Exercise 1.37. a. An infinite continued fraction is an expression of the form



As an example, one can show that the infinite continued fraction expansion with the Ni and the Di all equal to 1 produces 1/, where is the golden ratio (described in section 1.2.2). One way to approximate an infinite continued fraction is to truncate the expansion after a given number of terms. Such a truncation -- a so-called k-term finite continued fraction -- has the form



Suppose that n and d are procedures of one argument (the term index i) that return the Ni and Di of the terms of the continued fraction. Define a procedure cont-frac such that evaluating (cont-frac n d k) computes the value of the k-term finite continued fraction. Check your procedure by approximating 1/ using
(cont-frac (lambda (i) 1.0) (lambda (i) 1.0) k)
for successive values of k. How large must you make k in order to get an approximation that is accurate to 4 decimal places?

b. If your cont-frac procedure generates a recursive process, write one that generates an iterative process. If it generates an iterative process, write one that generates a recursive process.

Answer:
;; phi ~= 1.6180 (define (cont-frac n d k) (define (fraction i) (if (= i k) (/ (n i) (d i)) (/ (n i) (+ (d i) (fraction (+ i 1)))))) (fraction 1)) (define (phi k) (/ 1 (cont-frac (lambda (i) 1.0) (lambda (i) 1.0) k))) ;; For k >= 12 accuracy of four decimal places is obtained. ;; (phi 12) = 1.6180555555555558 ;; (phi 1000000) = 1.618033988749895 ;; Iterative version (define (i-cont-frac n d k) (define (iter i fraction) (if (= i 0) fraction (iter (- i 1) (/ (n i) (+ (d i) fraction))))) (iter k (/ (n k) (d k)))) (define (i-phi k) (/ 1 (i-cont-frac (lambda (i) 1.0) (lambda (i) 1.0) k))) ;; (i-phi 1000000) = 1.618033988749895
Exercise 1.38. In 1737, the Swiss mathematician Leonhard Euler published a memoir De Fractionibus Continuis, which included a continued fraction expansion for e - 2, where e is the base of the natural logarithms. In this fraction, the Ni are all 1, and the Di are successively 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, .... Write a program that uses your cont-frac procedure from exercise 1.37 to approximate e, based on Euler's expansion.

Answer:
;; Exercise 1.38 (define (calc-euler-e k) (define (euler-d i) (if (= (modulo (+ i 1) 3) 0) (* 2 (+ 1 (quotient i 3))) 1)) (+ 2 (i-cont-frac (lambda (i) 1.0) euler-d k))) ;; Expected e: ;; 2.71828 18284 59045 23536 ;; (calc-euler-e 10000) ;; 2.71828 18284 59045 5
Exercise 1.39. A continued fraction representation of the tangent function was published in 1770 by the German mathematician J.H. Lambert:



where x is in radians. Define a procedure (tan-cf x k) that computes an approximation to the tangent function based on Lambert's formula. K specifies the number of terms to compute, as in exercise 1.37.

Answer:
(define (tan-frac n d k) (define (iter i fraction) (if (= i 0) fraction (iter (- i 1) (/ (n i) (- (d i) fraction))))) (iter k (/ (n k) (d k)))) (define (tan-cf x k) (define (n i) (if (= i 1) x (square x))) (define (d i) (if (= i 1) 1 (- (* 2 i) 1))) (tan-frac n d k))
Exercise 1.40. Define a procedure cubic that can be used together with the newtons-method procedure in expressions of the form
(newtons-method (cubic a b c) 1)
to approximate zeros of the cubic x³ + ax² + bx + c.

Answer:
;; Cubic (define (cubic a b c) (lambda (x) (+ (cube x) (* a (square x)) (* b x) c)))
Exercise 1.41. Define a procedure double that takes a procedure of one argument as argument and returns a procedure that applies the original procedure twice. For example, if inc is a procedure that adds 1 to its argument, then (double inc) should be a procedure that adds 2. What value is returned by
(((double (double double)) inc) 5)
Answer:
(define (double f) (lambda (x) (f (f x)))) ;; (((double (double double)) inc) 5) = 21
Double is a function that takes an input function and returns another function which applies the input twice. Therefore (double double) returns a function that applies its input 4 times. (double (double double)) therefore leads to a function that applies its input 4 * 4, or 16 times. Applying inc 16 times to 5 yields 21.

Exercise 1.42. Let f and g be two one-argument functions. The composition f after g is defined to be the function x f(g(x)). Define a procedure compose that implements composition. For example, if inc is a procedure that adds 1 to its argument,
((compose square inc) 6) 49
Answer:
(define (compose f g) (lambda (x) (f (g x))))
Exercise 1.43. If f is a numerical function and n is a positive integer, then we can form the nth repeated application of f, which is defined to be the function whose value at x is f(f(...(f(x))...)). For example, if f is the function x x + 1, then the nth repeated application of f is the function x x + n. If f is the operation of squaring a number, then the nth repeated application of f is the function that raises its argument to the 2nth power. Write a procedure that takes as inputs a procedure that computes f and a positive integer n and returns the procedure that computes the nth repeated application of f. Your procedure should be able to be used as follows:
((repeated square 2) 5) 625
Hint: You may find it convenient to use compose from exercise 1.42.

Answer:
(define (repeated f n) (define (iter g i) (if (= i 1) g (iter (compose f g) (- i 1)))) (iter f n))
Exercise 1.44. The idea of smoothing a function is an important concept in signal processing. If f is a function and dx is some small number, then the smoothed version of f is the function whose value at a point x is the average of f(x - dx), f(x), and f(x + dx). Write a procedure smooth that takes as input a procedure that computes f and returns a procedure that computes the smoothed f. It is sometimes valuable to repeatedly smooth a function (that is, smooth the smoothed function, and so on) to obtained the n-fold smoothed function. Show how to generate the n-fold smoothed function of any given function using smooth and repeated from exercise 1.43.
(define (smooth f) (define dx 0.00001) (lambda (x) (/ (+ (f x) (f (+ x dx)) (f (- x dx))) 3))) (define (n-fold-smooth f n) (repeated smooth n) f)
Exercise 1.46. Several of the numerical methods described in this chapter are instances of an extremely general computational strategy known as iterative improvement. Iterative improvement says that, to compute something, we start with an initial guess for the answer, test if the guess is good enough, and otherwise improve the guess and continue the process using the improved guess as the new guess. Write a procedure iterative-improve that takes two procedures as arguments: a method for telling whether a guess is good enough and a method for improving a guess. Iterative-improve should return as its value a procedure that takes a guess as argument and keeps improving the guess until it is good enough. Rewrite the sqrt procedure of section 1.1.7 and the fixed-point procedure of section 1.3.3 in terms of iterative-improve.

Answer:
(define (iterative-improve good-enough? improve) (lambda (guess) (define (iter guess) (let ((next (improve guess))) (if (good-enough? guess next) next (iter next)))) (iter guess))) ;; sqrt using iterative-improve (define (ii-sqrt x) ((iterative-improve (lambda (guess next) (< (abs (- guess next)) tolerance)) (lambda (guess) (average guess (/ x guess)))) 1.0)) ;; fixed-point using iterative-improve (define (ii-fixed-point f first-guess) ((iterative-improve (lambda (guess next) (< (abs (- guess next)) tolerance)) (lambda (guess) (f guess))) first-guess)) ;; Calculating golden ratio phi ;; (fixed-point (lambda (x) (+ 1 (/ 1 x))) 1.0) ;; Requires 14 steps ;; = 1.6180327868852458

SICP Section 1.2 Procedures and the Processes They Generate

Exercise 1.9. Each of the following two procedures defines a method for adding two positive integers in terms of the procedures inc, which increments its argument by 1, and dec, which decrements its argument by 1.
(define (+ a b) (if (= a 0) b (inc (+ (dec a) b)))) (define (+ a b) (if (= a 0) b (+ (dec a) (inc b))))
Using the substitution model, illustrate the process generated by each procedure in evaluating (+ 4 5). Are these processes iterative or recursive?

Answer: First version is recursive; second is iterative. Exercise 1.10. The following procedure computes a mathematical function called Ackermann's function.
(define (A x y) (cond ((= y 0) 0) ((= x 0) (* 2 y)) ((= y 1) 2) (else (A (- x 1) (A x (- y 1))))))
What are the values of the following expressions?
(A 1 10) (A 2 4) (A 3 3)
Consider the following procedures, where A is the procedure defined above:
(define (f n) (A 0 n)) (define (g n) (A 1 n)) (define (h n) (A 2 n)) (define (k n) (* 5 n n))
Give concise mathematical definitions for the functions computed by the procedures f, g, and h for positive integer values of n. For example, (k n) computes 5n2.

Answer:
(A 1 10) ;; 2^10 = 1024 (A 2 4) ;; 65536 (A 3 3) ;; 65536 (define (f n) (A 0 n)) ;; (f n) computes 2n (define (g n) (A 1 n)) ;; (g n) computes 2^n (define (h n) (A 2 n)) ;; (h n) computes 0 if n = 0; 2 if n = 1; 2^h(n-1) for n > 1
Exercise 1.11. A function f is defined by the rule that f(n) = n if n<3 and f(n) = f(n - 1) + 2f(n - 2) + 3f(n - 3) if n> 3. Write a procedure that computes f by means of a recursive process. Write a procedure that computes f by means of an iterative process.
;; Recursive version (define (f n) (cond ((< n 3) n) (else (+ (f (- n 1)) (* 2 (f (- n 2))) (* 3 (f (- n 3))))))) ;; Iterative version (define (g n) (cond ((< n 3) n) (else (g-iter 2 1 0 (- n 2))))) (define (g-iter a b c count) (if (= count 1) (g-sum a b c) (g-iter (g-sum a b c) a b (- count 1)))) (define (g-sum a b c) (+ a (* 2 b) (* 3 c)))
Exercise 1.12. The following pattern of numbers is called Pascal's triangle. The numbers at the edge of the triangle are all 1, and each number inside the triangle is the sum of the two numbers above it.35 Write a procedure that computes elements of Pascal's triangle by means of a recursive process.

Answer:
(define (pascal row column) (cond ((= row 1) 1) ((= column 1) 1) ((= row column) 1) (else (+ (pascal (- row 1) (- column 1)) (pascal (- row 1) column)))))
Exercise 1.14. Draw the tree illustrating the process generated by the count-change procedure of section 1.2.2 in making change for 11 cents. What are the orders of growth of the space and number of steps used by this process as the amount to be changed increases?

Answer: Amount (steps and space) are respectively 1 (10), 2 (12), 3 (14) etc. Therefore space and # of steps grows linearly with amount. O(n).

SICP section 1.1 The Elements of Programming

Exercise 1.1. Below is a sequence of expressions. What is the result printed by the interpreter in response to each expression? Assume that the sequence is to be evaluated in the order in which it is presented.
10 ;; 10 (+ 5 3 4) ;; 12 (- 9 1) ;; 8 (/ 6 2) ;; 3 (+ (* 2 4) (- 4 6)) ;; 6 (define a 3) ;; <nothing is printed> (define b (+ a 1)) ;; <nothing is printed> (+ a b (* a b)) ;; 19 (= a b) ;; #f (if (and (> b a) (< b (* a b)) ) b a) ;; 4 (cond ((= a 4) 6) ((= b 4) (+ 6 7 a)) (else 25) ) ;; 16 (+ 2 (if (> b a) b a)) ;; 6 (* (cond ((> a b) a) ((< a b) b) (else -1)) (+ a 1) ) ;; 16
Exercise 1.2. Translate the following expression into prefix form

(/ (+ 5 4 (- 2 (- 3 (+ 6 (/ 4 5))))) (* 3 (- 6 2) (- 2 7)) )
Exercise 1.3. Define a procedure that takes three numbers as arguments and returns the sum of the squares of the two larger numbers. (define (smallest x y z) (cond ((and (>= x z) (>= y z)) z) ((and (>= y x) (>= z x)) x) ((and (>= z y) (>= x y)) y) ) ) (define (square x) (* x x)) (define (sum_of_squares x y) (+ (square x) (square y) ) ) (define (sum_of_squares_of_larger_two x y z) (cond ((= (smallest x y z) x) (sum_of_squares y z)) ((= (smallest x y z) y) (sum_of_squares x z)) ((= (smallest x y z) z) (sum_of_squares x y)) ) )
Exercise 1.4. Observe that our model of evaluation allows for combinations whose operators are compound expressions. Use this observation to describe the behavior of the following procedure: (define (a-plus-abs-b a b) ((if (> b 0) + -) a b))
Answer: The procedure a_plus_abs_b takes two arguments, a and b. It evaluates the expression (operator a b) where operator is chosen as either + or - depending on whether b is greater than zero or not. The key is that operator itself is the value of evaluating the if expression.

Exercise 1.5. Ben Bitdiddle has invented a test to determine whether the interpreter he is faced with is using applicative-order evaluation or normal-order evaluation. He defines the following two procedures: (define (p) (p)) (define (test x y) (if (= x 0) 0 y))
Then he evaluates the expression (test 0 (p))
What behavior will Ben observe with an interpreter that uses applicative-order evaluation? What behavior will he observe with an interpreter that uses normal-order evaluation? Explain your answer. (Assume that the evaluation rule for the special form if is the same whether the interpreter is using normal or applicative order: The predicate expression is evaluated first, and the result determines whether to evaluate the consequent or the alternative expression.)

Answer: If applicative order is used for evaluation the arguments to test are evaluated first. This means (p) is evaluated, leading to an infinite loop. On the other hand with normal order evaluation (p) is not evaluated until it is actually needed. Since the if is designed in such a way that this never happens, there is no infinite loop and the call returns 0.

Exercise 1.6. Alyssa P. Hacker doesn't see why if needs to be provided as a special form. ``Why can't I just define it as an ordinary procedure in terms of cond?'' she asks. Alyssa's friend Eva Lu Ator claims this can indeed be done, and she defines a new version of if: (define (new-if predicate then-clause else-clause) (cond (predicate then-clause) (else else-clause)))
Eva demonstrates the program for Alyssa: (new-if (= 2 3) 0 5) 5 (new-if (= 1 1) 0 5) 0
Delighted, Alyssa uses new-if to rewrite the square-root program: (define (sqrt-iter guess x) (new-if (good-enough? guess x) guess (sqrt-iter (improve guess x) x)))
What happens when Alyssa attempts to use this to compute square roots? Explain.

Answer: Normally if evaluates the alternative only if the predicate is false. This is why it is a special form. Since Alyssa's version is not a special form the alternative is evaluated irrespective of the result of the predicate. In the case of square roots this means calling sqrt-iter again, leading to an infinite loop.

SICP: Solutions to Exercises and Notes

I started my sabbatical in early July 2008 with the aim of working through the Structure and Interpretation of Computer Programs, exercises and all. I have completed the first three chapters at the time of writing this. So far I have been posting notes at the end of each chapter. I'll now start putting up my solutions to the exercises and any notes/questions I have.

All the exercises have been written in MzScheme using DrScheme. DrScheme's implementation of MzScheme worked straight out of the box for most purposes. The only serious tweaking I had to do so far was to add a macro for the cons-stream operation required in chapter 3. The code for this macro was borrowed from the PLT Scheme mailing list.

Testing Code Highlighting Redux

I have been playing around with adding syntax highlighting for Scheme using syntaxhighlighter (albeit an old version of the tool). Here is a little test to see if it worked. (define (probe name connector) ;; comment (define (print-probe value) (newline) (display "Probe: ") (display name) (display " = ") (display value)) (define (process-new-value) (print-probe (get-value connector))) (define (process-forget-value) (print-probe "?")) (define (me request) (cond ((eq? request 'I-have-a-value) (process-new-value)) ((eq? request 'I-lost-my-value) (process-forget-value)) (else (error "Unknown request -- PROBE" request)))) (connect connector me) me)

Sabbatical Update #3

I completed Chapter 3 of SICP today. It took longer than expected but was worth the effort I put in.

Chapter 3 started off by introducing state variables. This was quite new for chapters 1 and 2 used stateless procedures to solve problems. With the introduction of state came new problems. The substitution model of evaluation was no longer adequate to figure out how a given procedure would work. The authors introduced what is called the Environment Model as a better suited means of evaluation. The new model made good use of environment diagrams to help the process. In fact many exercise problems require the student to come up with environment diagrams along with the actual procedures.

The authors then focused on a prominent outcome of using assignment - mutable data. This involved learning to work with mutable lists and designing implementations of queues and tables. The understanding of mutable data and data structures were put to use in solving problems related to simulating digital circuits and constraint propagation.

The next section demonstrated the problems created when assignment and concurrency collide. Serialization was discussed in some depth as one possible way to control problems related to concurrency. I learned to implement simple mutexes and serializers.

The last section of the chapter - Streams - proved to be the most interesting and conceptually difficult to understand. In general streams are data structures used to represent sequences. They are distinct from lists in that they make use of delayed evaluation. What makes them fascinating is how such a powerful concept is built using such simple ingredients as force and delay.

Streams proved to be difficult to tackle in the beginning. The breakthrough came when I learned to ignore the syntax (the force and delay bits in particular) and look at streams purely as sequences, sometimes mathematical ones. Understanding stream operations became easier once I visualized these operations as "machinery working on moving assembly lines".

Comic Books and Graphic Novels

During a recent conversation a friend asked me about the difference between a 'Comic Book' and a 'Graphic Novel'. This was not the first time I had heard the question. Usually people wanted to know what I mean by 'graphic novel'. One gentleman wanted to know if I was using the phrase graphic novel to cover up the fact that I read comic books.

I'll take the second question first. I was surprised that someone would consider an adult reading comic books as unusual (unbecoming?). Perhaps I shouldn't have been so surprised given that I was talking to someone in the software industry, but I digress. In any case I was not trying to "cover up" my reading tastes by using the phrase. I buy and read graphic novels and comics openly; I don't hide my copies of Watchmen, V for Vendetta or Asterix, to name a few. I rank some of them among the best books I have read.

Why then distinguish between comic books and graphic novels? In my mind the distinction is not so much between children's and adults' reading but between the content and presentation. Take for example the 2005 movie Batman Begins. Contrast it with the 1985 vintage Batman. Both are based on the same comic book superhero and narrate similar stories. In spite of their similarities they both are significantly different products. The former is the movie equivalent of a graphic novel while the latter is firmly rooted in the comic book tradition. 'Begins' gained a far wider audience for the reason that it was a very enjoyable movie that happened to be based on a superhero. 'Batman' on the other hand was a movie that played mostly to the crowd already familiar with the story and were in the theater to watch a film adaptation.

The distinction is arguably subjective. I will list below the factors I use to differentiate a comic book from a graphic novel.

1. Non-traditional characters. Where traditional comic books have mostly focused on superheroes (with or without superpowers) graphic novels have told the stories of such mold-breaking characters like the Swamp Thing and John Constantine.
2. Different treatment of existing characters. This is most vividly illustrated by the success of recent movies like The Dark Knight. These movies were inspired by various graphic novels which told vastly new tales featuring familiar characters, sometimes casting them in an entirely new light.
3. Shorter, non-serial story arcs. Comic books typically use recurring characters and story lines that extend across lengthy arcs. Graphic novels are closer to traditional novels in that their story arcs are shorter. Classic examples include Alan Moore's V for Vendetta and Watchmen. This is not always true though; Neil Gaiman's Sandman spans multiple episodes, as do graphic novels featuring Batman.
4. Non-uniform presentation. Traditional comic books tend to have a relatively uniform look even when created by different artists. Graphic novels are known for using different artists with pronouncedly different styles in the same volume. The Sandman series is a good example.
5. Stylized depiction. This is related to the point mentioned above. Many Graphic novels use fantastically stylized depictions of characters. Frank Miller's Dark Knight, Sin City and 300 come to mind.
6. Reading experience comparable to traditional novels. This is quite subjective. I find the experience of reading graphic novels more comparable to reading traditional literature. Take for instance the character Death from Neil Gaiman's Sandman universe. I found that the two spin-off volumes featuring Death read like engrossing short stories.

SICP: Thinking Aloud

I am presently working on the third chapter of SICP. I found the opening section about environments and maintaining local state particularly interesting. After working through the exercises for the first two sections I started paraphrasing the authors' explanations in my mind to see if I had really understood the concepts. Most ideas were non-trivial but became malleable once I put in enough effort. However one particular exercise threw up questions that I could not clearly answer.

Here is some context to start with.

I know of two ways to define a procedure, say to square a given number, given below:

    ;; Form #1
    (define (square x) (* x x))

    ;; Form #2
    (define square (lambda (x) (* x x)))

Neither definition maintains state and both yield identical results for identical inputs. So far so good. Now consider the following procedure definition.

    (define f
      (let ((state 1))
        (lambda (x) (set! state (* state x)) state)))

    (+ (f 0) (f 1)) ;; returns 0
    
    ;; Reset interpreter and run with order of arguments to + reversed
    (+ (f 1) (f 0)) ;; returns 1

This procedure is easily explained. It maintains a local state variable initialized to 1. Inputs to the procedure are multiplied by the state, the existing state variable is replaced by the product and the new value of the state variable is returned. Consequently if the input to the procedure is ever 0 then the procedure will return 0 for all subsequent inputs. The state is not in the global environment but a local environment "attached" to the procedure. This local environment is easier to visualize when the let construct is replaced with an equivalent lambda expression.

    (define f
        ((lambda (state) (lambda (x) (set! state (* state x)) state)) 1))

My problems began when I tried to convert this definition to the "regular" form, i.e. (define (f x) ...). I tried the following, with and without the let construct:

    (define (f x)
      (let ((state 1))
        (set! state (* state x))
        state))

I was not sure if this would work; evaluating the test expressions quickly confirmed my suspicions. The two definitions were NOT equivalent. Unlike the first form the "regular" form did not seem to maintain state across invocations. Here is my understanding of what is happening.

When the procedure body is evaluated the value of state is set to 1 in the corresponding frame. The state is indeed changed to the product using the set! call. However nothing is changed in the "nearest" environment, which is the global environment. The frame is discarded when the procedure terminates and the state is lost. In the earlier case the attached local environment stayed alive even after the procedure terminated thereby enabling it to preserve state.

To test my theory I moved the state variable to the global environment. Everything worked as expected thereafter.

    (define state 1)

    (define (f x)
      (set! state (* state x))
      state)

My explanation notwithstanding, two questions remain.

1. Is my understanding correct?
2. Is it possible to convert the procedure from one form to another without resorting to defining state globally? If so, how?

I hope that my questions will be automatically answered as I learn more. In the meantime please let me know if you have any thoughts on the topic.

PS: Thanks to Magicindian for helping me to derive my questions from what started out as a vague tangent of the solution to an SICP exercise. He has a particular talent for distilling clear and concise ideas from tangled masses of thoughts. He gave me several useful inputs which I neglected to write down. I promise to keep notes the next time I have interesting discussions with my friends and report them along with the final summary.

Sabbatical Update #2

I completed Chapter 2 of SICP yesterday. I am taking the day off from my regularly scheduled activities to rest and recuperate and also to write this mini-report.

While chapter 1 was definitely interesting the second chapter was far more meatier in terms of fundamental concepts presented and explored. I have written code mostly in Python and Java and had very conventional notions of 'data' in the programming context. The authors of SICP challenge that notion almost right from the beginning of the chapter. They present - and illustrate - the idea that data can be thought of as "some collection of selectors and constructors, together with specified conditions that these procedures must fulfill in order to be a valid representation". The rest of the chapter builds on this fundamental concept working on more complex data including a mini "picture language".

It took me some time to digest this idea and longer to deal with some of the exercises. One particular exercise involved implementing Church Numerals using Scheme. Church Numerals are the brain child of mathematician Alonzo Church who first described a way to embed data and operators into lambda calculus. I thought the name 'Church Numerals' was a misnomer seeing that these were not 'numerals' in any way I have come to understand :-P Jokes aside the exercise was thought provoking. In case you were wondering this is what "0" and "1" look like:

    ;; zero
    (define zero (lambda (f) (lambda (x) x)))

    ;; one
    (define one (lambda (f) (lambda (x) (f x))))

I later realized that my troubles arose from my focus on the form of numbers rather than the function they served. Once I understood the distinction between the two it became easier to address the problem.

On a related note I will be putting up my solutions to the SICP problems shortly, starting with Chapter 2.

Another Recital and Related Thoughts

I played the Piano at a small recital organised in my teacher's home last month. This was my second recital this year. I played two pieces - Theme and Variations by Theodore Kullak and Rocking Horse Ride (Opus 98, No. 5) by Alexander Gretchaninov. Kullak's piece presents a theme followed by five variations of that theme. The hand positions are fixed and the tempo increases in the fourth and fifth variations. 'Rocking Horse Ride' is taken from Gretchaninov's 'Children's Book'. It tells about a rocking horse that starts off slowly enough but soon accelerates and almost rocks too far. But all is well in the end.

The single most important difference from my previous recital was my increased confidence. This was not entirely surprising given that I had prepared myself better this time around. It helped that I had been out of work for a couple of weeks before D-Day. And I forced myself to take a quick nap in the afternoon before the event. It was a refreshing contrast from the previous before-recital afternoon when I was tightly wound up and excited.

All of it paid off in the end. I did not mess up any notes but I did feel that I could have done better on the dynamics.

On a related note I was told that my music practice had noticeably improved ever since I left my job. This was a bit surprising especially since I had not drastically lengthened my practice sessions. I think reduced stress levels made most of the difference. In retrospect I can see that work had been so draining that I had become used to being perpetually wound up and did not notice how it was degrading the quality of my life.

I don't seem to be the alone in being stressed out. I learned from my teacher that there was a time when recitals were far more frequent. According to her pupils these days (that includes me) take much longer to get ready for a recital. She stressed how barely half a generation ago pupils - who were also at school, had a job or were otherwise busy - were somehow able to find time to do justice to music. With every passing year pupils seem to have less and less time to practice, or indeed to focus on anything much outside work.

I have decided to actively combat stress the next time I start working a job. This would mean working regular hours, leaving work behind on stepping out of the office, learning to turn off my phone after hours and during weekends. I don't know how I'll achieve all these but I certainly am not going to let work deprive me of life again.

State of the Sabbatical

Yesterday marked the end of the first month of my sabbatical. I used the opportunity to sit back and take stock of how far I have progressed towards achieving my goals. For the record I started on my sabbatical aiming to achieve the following before November:

1. Work through Structure and Interpretation of Computer Programs (SICP), exercises and all
2. Learn to play Muzio Clementi's Sonatina in C Major (Opus 36 No. 1) well enough to give a recital
3. Read one (non fiction) book every fortnight

Here follows then a quick summary of the state of the sabbatical.

At the time of writing this I have completed the first of five chapters of SICP and started on the second. I am presently working on the second of three movements of the Sonatina. I finished reading 'The Audacity of Hope' and am looking for another book.

Working through SICP is proving to be an eye opener. The exercises look deceptively simple until you try to work them out. I was *very* frustrated in the beginning but am learning relax and re-focus. Some of the ideas took a while to wrap my mind around due to various factors. I had never worked in Scheme before and found it difficult to write programs without explicit looping constructs and variable assignment. For this reason the Chapter 1 exercises dealing with converting recursive procedures to iterative and vice-versa troubled me for several days. I was shocked to notice how long it took me to understand and digest fundamental concepts like lambda. Easy work in enterprise software for 8 plus years seems to have damaged most of my gray cells :(

The Sonatina is proving tough to crack. The first movement was relatively simple. But then came the second movement with its triplets, trills and one-sixteenth notes. It quickly deprived me of the warm glow of working through the first. So far I have hammed my way through five lines. The last line is adamantly refusing to submit.

'The Audacity of Hope' is a very engrossing read. It is rare to see a politician writing for himself without relying on ghost writers. It was evident after reading the book that Senator Obama can not only write for himself but matches his words with sharp thought and keen observations.

That is all in this week's report. More soon.

Stuck in a Time Frame

The topic of some mutual friends came up during a recent conversation I had with a friend. After I filled her in about their whereabouts and activities she remarked that said friends and yours truly were "stuck in a time frame". I understood what she meant in the context of our conversation. I realised that she had merely expressed in a catchy phrase an opinion others had expressed before using different words. In order to fully understand the import of 'stuck in a time frame' I will first try to illustrate its opposite concept. 'Moving through time frames', if you will.

The basis of my explanation is my understanding that the (suburban, educated) Indian society expects individuals to live their life in a certain way based on their age "time frame". In Kerala the teen years are considered to be the time for education. You are expected to be in college by your late teens. Some of the non-curricular pursuits of a typical student include dabbling in new hobbies and other activities. These are mostly but not always tolerated. For instance I picked up Miniature Wargaming as a hobby in college. I hasten to add that individuals are expected to outgrow their hobbies or interests as they move on to the next stage in life.

For my generation a person's twenties is the time for seeking gainful employment, sometimes after completing higher studies. As travelling overseas became more common and affordable people were expected to switch to "explore" mode after landing a job. Non-curricular activities of this time frame include visiting various places, picking up hobbies that are made more affordable by technology etc. Most notable among the latter is Photography. Of course there are people I know who used to save their allowances to make money for Photography while in college but that is another story.

Mid to late twenties, as I was told by more than one person, is the time to move on again. Marriage is *the* key social event marking the end of this time frame. This is such a strong social expectation that unmarried people are treated almost as if they are in mortal danger and pose a threat to others. It is common for bachelors and spinsters to be asked even by virtual strangers why they haven't married. Marriage itself is the outcome of a filtration process demanded by society and community and initiated by parents. Criteria of filtration include religion, caste, community, state, and language to mention a few. A list of desirables passing the filter conditions is presented to the "end user" and he or she can pick any one. There indeed are exceptions but these remain a very small minority.

A man in his thirties is expected to start a family and "engage society more actively". "Engaging society" means, among other things, actively participating in social events that you were given permission to avoid as a twenty-something. Hobbies are frowned upon unless they are strictly mainstream. Non work related pursuits are allowed as long as they are for buying a new car, apartment or real estate.

I don't know quite clearly what my generation is expected to do in our forties, fifties and subsequent decades. I speculate that our forties would be the time to focus on children and career growth punctuated by the occasional mid life crisis. The fifties would be time to coordinate marriages of children born to the Indian software generation.

It is interesting to note how a bit of this progression is reflected in the photo galleries of a social networking site popular with Indians. First, snaps of the protagonist in various places around the globe. Some capture their first car or apartment. Marriage photos and pictures of the sweetheart appear some time later. These are in turn replaced by pictures of children and group photographs.

Coming back to my conversation I found that my friend's opinion was apparently based on her observations of the individuals' lives. None of the people we discussed including yours truly had "moved on" as she expected. At least two in the list are pursuing higher studies in their thirties, that too in subjects not necessarily related to their present careers. Three are not married and don't plan to. Not to mention their hobbies. I counted several different hobbies in the group ranging from dancing to miniature wargaming to semi-professional poker to playing the Mridangam.

I told my friend that all the people we discussed had merely chosen to define the (time) segments making up their life differently. I was not convinced by her arguments that one should drastically change his outlook on life for the sole purpose of meeting popular definitions of "moving on". As far as I see each one of these people *have* been moving on. They are more skilled, know more about their favourite subjects now than they did five years ago and are by no means staying still in any of their chosen fields of endeavour. If anything almost all of them rue that they are not moving forward as fast as they would like to.

A Tale of Two Movies

The acclaimed Malayalam movie 'Paithrikam' came out in 1993, the year I finished school. Directed by Jayaraj the movie told the story of two generations of a Kerala Brahmin family. The father is a soft spoken orthodox Brahmin well respected in the community and a learned scholar-performer of rituals and Yajnas. His eldest son is a vocal atheist who is openly against theism in all its forms including his family's rituals and cloistered lifestyle. Caught between the two are a loving younger brother and a largely silent mother. The movie builds towards a confrontation between the beliefs of father and son culminating in a final act where the son undergoes a spiritual conversion and takes his father's place.

The movie is commendable on its own merits. However I remember it for different reasons. As a Brahmin I witnessed first hand how 'Paithrikam' became quite popular in the Brahmin community shortly after its release. For a while after the movie came out its name came up during conversations in many families including mine. Relatives had good things to say about the movie at family gatherings. I distinctly recall seeing advertisements for the movie endorsed by prominent Brahmin priests and scholars. These usually said something like "I strongly recommend everyone to watch it" or "a poignant narrative". I believe that for some people the movie came as an affirmation of their strongly held beliefs about the "superiority" of Brahmin culture and tradition. Some perceived the movie to be in agreement with their reservations against atheism and progressive trends in the community.

I will not discuss the merits of such beliefs but instead skip ahead to narrate the tale of another movie that came out barely a year later. Hariharan's 'Parinayam', scripted by veteran Malayalam writer M.T. Vasudevan Nair also centred on a Brahmin family. The movie was set in the turbulent decades of late 19th and early 20th centuries that witnessed several changes in India's social order. The events portrayed in the movie occur not long after the Kerala Brahmin community was scandalised by the ritual trial of a Brahmin widow Savithri, alias Thathrikkutty, for adultery. The accused named no less than sixty four prominent persons from different castes as her lovers. This was also the time when progressives led by reformers like V.T. Bhattathirippad organised a movement against social ills prevalent in the Brahmin community.

'Parinayam' is the story of a young Brahmin girl who becomes the fourth wife, and widow shortly thereafter, of an old Brahmin lord. She becomes pregnant after her husband's death and is tried by a communal tribunal. The movie ends with her being cast out from home and community and starting an independent, defiant life with the help of her rebel/reformer stepson.

Here again the movie shines and can be enjoyed for its own merits. What I want to point out however is how this movie was hardly ever mentioned by the same people who were all praise for the earlier one. Going strictly by quantity and extent of Brahmin traditions portrayed the second movie should have attracted a much wider audience. And yet it failed to be even so much as mentioned in gatherings, much less admired.

Why this difference? I thought about this after I watched 'Parinayam' again very recently. I think that many in the Kerala Brahmin community are guilty of selective adoption and propagation of events defining its History. The dark tales are entirely left out when the story of a vibrant socio-religious past is told. Consequently many youngsters grow up with a skewed knowledge of history which only serves to enforce their illogical belief in superiority by virtue of birth in an "upper" caste.

In this context it is interesting to inspect how the community organisation formed by Bhattathirippad to combat social ills has evolved. What once was the refuge of rebels and progressives is now the gathering place for conservatives and the orthodox. Where membership was once a statement of rebellion today it is a bellwether of social prominence.

I have a firmly held belief that a person's caste has nothing to do with how good or bad a person he is. My beliefs aside I still wish that those who give importance to belonging to a community were more objective in drawing lessons from its past. For it is a fact of history that for every 'Paithrikam' there are all too many 'Parinayam's.

Extreme Programming in Action

Extreme Programming has become more "mainstream" in the Indian software industry over the past couple of years. For many companies their agile development practices have provided a reason to brag and to attract recruits. One of my friends works for such a company and recently narrated an incident highlighting how "XP" is used in his workplace. I thought I should share it with the rest of the world to provide another perspective on how XP is actually used in Bangalore.

The specific case involved a particular task which came up for development. One of the developers said that it would take him 2 days to finish the task while another thought he could complete it in 3 days. A third predicted four days if he were to do the task. The team leader heard them all out and proceeded to *assign* the task to the third guy. If you are thinking "that's not how it is done in XP" - wait, the best is yet to come. The "leader" expected the "assigned" developer to finish the task in 2 days!

From what I heard the practice is not only widespread in the said organisation but some managers actually *coach* sceptical newcomers to believe that this "auction model" is a core tenet of XP. Those who disagreed are reprimanded for unwillingness to adhere to XP.

The next time someone from this place says "we follow XP" I am going to burst a gut laughing :)

Of Festivals

March, April and May have traditionally been "festival months" in Kerala. Many Hindu temples (as well as a few houses of worship of other religions) celebrate socio-religious festivals during this season which also witnesses the turn of the Malayalam year. My trip home to Trivandrum earlier this month coincided with the annual festival at a nearby temple. It has been close to a decade since I was last home in time for the occasion. Several things have changed since then. Most notably the noise output has gone up considerably. Loudspeakers heralding the event covered an area approximately 1 Km in radius. As my house is well within this radius I got to hear music (live and recorded, instrumental and vocal), announcements, religious talks and other sounds almost around the clock. My five day visit completely overlapped with the festival's duration of 7 days to the effect that I was almost always raising my voice to talk to my family.

The loudspeakers usually came to life around 6.00 in the morning, more than an hour after the temple opened for the day. They would then blare "devotional songs" for the next three hours or so. The music was periodically interrupted for announcements. Going by voice these were all made by the same person. The announcer typically started by reciting the day's programme. He would then go on to thank individual donors whose contributions went towards paying for the day's events. Names, addresses and the events which benefited were included. He usually ended with a religious greeting.

The speakers were given a break around 10.00 AM coinciding with religious rituals in the temple. Unfortunately this break lasted barely an hour. The next "session" commenced with yet more songs and traditional instrumental music unless there happened to be a religious talk going on. Following another short break around noon the fare would continue well into the afternoon. Unexpected relief arrived on a couple of occasions thanks to the trusty summer afternoon rains. The lightning accompanying the showers forced the operators to shut down their makeshift Public Address system albeit for a short while.

The noise levels went down whenever a ritual was performed in the temple premises. After the main worship ceremony around 6.00 PM the racket would continue well into the night thanks to the "main cultural event" of the day. Such events tended to live performances of music, dance or comedy with the rare Kathakali session thrown in for traditions' sake. Plays and movies used be a part of the fare ten years ago but have since been dropped. Live performances typically ended by 1.00 AM and the PA system shut down shortly thereafter. On one particular occasion however the music accompanying a Kathakali performance started around 10.00 PM and went on until after 4.00 AM the next morning. The best part was when the announcer came on right afterwards to announce - what else - the names and addresses of the donors! I have since been told that most donors actually expect their names to be aired prominently and repeatedly in exchange for their contributions.

The last day of the festivities was marked by a procession featuring decorated elephants. The procession left the temple in the evening and returned sometime after midnight. The sound of the traditional drums accompanying the procession was broadcast for a while until a solitary voice took over to chant "Om....." repeatedly. The chanting lasted for half an hour while the procession re-entered the temple.

Interestingly several otherwise sensitive people seemed not to mind the noise pollution. These were the same folks who bristled when a political party dared to broadcast musical propaganda or speeches for a half day long meeting. One of the supporters argued that there could be no comparison between "devotional music" and "political music". My argument that both impinged on the personal comfort of those not interested was dismissed with a wave of the hand.

I believe this question was posed before the courts some time ago. The only solid outcome of such litigation has been the replacement of old, noisy, ultra polluting horn speakers with modern box models. Very few abide by the prescribed decibel levels and timings.

Meeting Dijkstra

I spent the last couple of weekends implementing Dijkstra's Shortest Path algorithm in Java. DSP is a fairly straight forward algorithm built on simple steps. Nevertheless I found it trickier than expected to convert it to code, my "work experience" and familiarity with Java notwithstanding. In the end I was able to work out a reasonable implementation after going through a few iterations.

I realised that in spite of working daily on a large body of code I was out of shape programming wise when it came to implementing algorithms. Part of the reason is my own average skill level; part of it is how rarely I tangle with algorithms at work. I suspect that this is the case with most programming jobs in town. There are other reasons as well not least of them being that algorithms require considerable thought to translate to code.

One of the interesting problems I faced had concerned representing the domain in code. For instance DSP works on Graphs made up of Vertices connected by Edges. It was fun to work out how to represent a Graph programmatically. In the end I chose method #1 suggested by Cormen et al., namely maintain Adjacency Lists.

Overall I found getting back in touch with the fundamentals an enjoyable experience. I plan to take this exercise further over the course of the next six months by working through Introduction to Algorithms. In the end I hope to emerge with a better understanding of the fundamentals.

A Sabbatical Test

One of my friends recently acted on his wish to take some time off from work. He just started a three month break from work. Every now and then I think about taking some time off from work myself. After watching my friend leave town for his sabbatical I gave the topic some active consideration. I realised that while the idea of taking time off from work was very tempting I would have to plan extensively to make it serve my purpose. Following a thought exercise I came up with a check list of things to accomplish before I can take time off. Note that the ordering is random.

1. Build A Monetary Base. I should have enough dough in the bank to cruise for the duration of my sabbatical. The time frame I have in mind is about a year. Whether I plan to leave Bangalore or stay in town makes a big difference in the estimate. I can think of a couple of other places that are cheaper but have other, outweighing disadvantages. For instance Chennai is too hot, Trivandrum is too remote and I don't know anyone in Pune :)

2. Plan Ahead. I have wasted far too many weekends for lack of proper planning. I do not wish to repeat this mistake during my sabbatical. I will have to work out a clear, weekly (or at least monthly) plan before I start my break.

3. Establish Habits In Advance. This follows from #2. I know from experience that even optimistic plans fail because I am not used performing a particular set of tasks regularly. Mental exercise is similar to physical exercise in this context. Even a modestly mind-intensive schedule needs a period of "warming up". I would rather do all the warming up work before I start rather than use the first days/weeks/months of the sabbatical for the same. This involves enforcing basic habits like going to bed and getting up at regular times, not getting "lost" for (unplanned)hours in a task however exciting it is etc.

4. Establish A Ready-to-expand Routine. This derives from #2 and #3. I spend around 10 hours at work each day including getting there and back. While all non-work activities look very attractive from the workplace it is not easy to effectively use the 10 hour or so of daily unstructured time that follows leaving work. One solution for the weak minded like me would be to establish in advance a routine that is "ready to expand". In other words I should use the time available to me *after work* every day to the maximum extent possible. Ideally this should lead to a point where any time off from work would be easily filled by one or more of the activities I have been doing.

Good examples include music practice and coding. Say I can spare 90 minutes for music practice each day, split into two 45 minute sessions before and after work. If I can take up a suitably complex piece that demands more than 90 minutes daily and work on it regularly for exactly 90 minutes a day then I would be making progress on conditions #3 and #4.

Similarly I should be able to pick up a a challenging programming goal and spend a fixed quantity of time, say 90 minutes, each day for a suitably long period.

Another important aspect in my case would be to perform *all* tasks *every* day. I don't think it would be realistic to divide a sabbatical into two or more consecutive periods where I only work on any one thing at a time. IMHO the key to making a sabbatical work is to make a little progress on all fronts every day.

5. Set "Service Level Agreements" For Friends And Family. IMHO a sabbatical is *not* a vacation. It is a life project with specific time duration and goals. I should make it clear to friends and family that just because I am "out of a job" they shouldn't expect me to spend additional time/energy thus gained on lengthy visits or other activities. If anything I expect to be busier during a sabbatical than I would have been while working.

Update: One of my friends who wishes to remain anonymous had this useful point to add: "Having a test (to be taken at the end of the period or at specific times) to check whether the purpose of the sabbatical has been achieved will be useful too. The act of coming up with the test will bring the why (take the sabbatical) question into focus. I suppose this will be an outcome of the planning activity."

Recital

I played the Piano at a small recital organised in my teacher's home last Sunday. My piece was a Sonatina in C Major (Opus 34, No. 1) written by Johann Anton André. The piece has two movements, a song like moderato followed by a lively Rondo. The event came at the end of slightly more than a year of lessons. Last year at a similar event I was a novice sitting with the audience marveling at the performances. This year it was my turn to get behind the keys.

Unfortunately for me two of my friends were in attendance in spite of my best efforts to prevent them from coming. When my turn came I found myself quite nervous to even approach the "stage", in this case the piano in the middle of the living room. This came as a surprise. I was a public speaker in college and in spite of my many faults have never had a case of stage fright. Playing a well rehearsed piece for 25 odd people should have been easy, but wasn't because I was very anxious about missing a note or phrase.

As it turned out I ended up making mistakes in a couple of places in the first movement. I did not die on the spot; on the contrary I began to relax after completing the first few lines. The second movement went fairly well even if I say so myself.

I don't recall much about the audience reaction. I do recall that my friends did not boo but then they were not experienced enough to have recognised my mistakes :) Tasty refreshments were served afterward but my body was awash in adrenalin for me to work up much of an appetite.

In retrospect the recital was a good experience. It made me realise the need for any student of music to periodically perform in a (semi-)public setting. I would like to be a part of more such events in the future. These need not even be on the same scale as my recital. A group of four or five would suffice. Perhaps these events can be arranged along the lines of the very useful "losers club" meetings I have attended. I can think of several advantages of such gatherings. Besides bolstering their confidence attendees also get valuable feedback. The "mini-recital" format would force all to focus on coming up with measurable output (play a piece) as opposed to talking about it ("I practiced for a total of 15 hours last month"). I am talking to a couple of musically inclined friends to see if we can come up with something worthwhile. Let me see how it works out.

What am I writing?

I started the year with a resolution to write more frequently. Specifically I had set myself a goal to write four blog entries a month and thereby work up a total of 52 by the end of the year. As the second month draws to a close I am three entries short (if I count this one as well) and trying hard to catch up. The question is, what do I write about?

I had a discussion with a friend where the same question popped up. I mentioned that I was not sure what to write. He suggested that I ask myself this question: "What would I discuss with a friend if we had 30 minutes to spare?". The question yielded instant results (not entirely surprising given my propensity to talk). There are indeed a bunch of things I would like to talk about with my friends. Here is a partial list.

• Learning (How to have a day job *and* find time and energy to learn; learning "methodologies")
• Programming (how to use it as a tool to help learning)
• Hobby - Miniature Wargaming
• Hobby - Music (practice, objectives, tips and tricks)
• Tackling the rest of my life (Post Three-Oh blues)
• Movies and Books
• History
• Current Affairs
• Living in Bangalore
• Travel plans

You may have noticed that whatever I have written so far falls under just a few topics in the above list. In retrospect it is evident that I have been writing only about those topics which I thought "people would want to read about". This is not helpful for many reasons. First of all it forced me to think about guessing what "people" liked to read rather than focusing on what *I want to write about*. Such a filter also impeded writing frequently and making enough mistakes to learn from and improve.

Also I have found that writing something down crystallises my thoughts. The absence of writing frequently leads to vague, half-baked ideas and thoughts.

To make up for my mistakes I have decided to actively implement my resolution in the coming weeks and months. I will try my best to write at least one entry a week. Expect to see me back shortly.