Answer:
length and list-ref functions described in the text.Exercise 2.18. Define a procedure reverse that takes a list as argument and returns a list of the same elements in reverse order:
Answer:
Exercise 2.19. Consider the change-counting program of section 1.2.2. It would be nice to be able to easily change the currency used by the program, so that we could compute the number of ways to change a British pound, for example. As the program is written, the knowledge of the currency is distributed partly into the procedure first-denomination and partly into the procedure count-change (which knows that there are five kinds of U.S. coins). It would be nicer to be able to supply a list of coins to be used for making change.
We want to rewrite the procedure cc so that its second argument is a list of the values of the coins to use rather than an integer specifying which coins to use. We could then have lists that defined each kind of currency:
We could then call cc as follows:
To do this will require changing the program cc somewhat. It will still have the same form, but it will access its second argument differently, as follows:
Define the procedures first-denomination, except-first-denomination, and no-more? in terms of primitive operations on list structures. Does the order of the list coin-values affect the answer produced by cc? Why or why not?
Answer:
Order of the list
coin-values will not matter. This owes to the way cc is structured. The first recursive call to cc tries to compare the amount with *all* denominations irrespective of their order in the list.
Exercise 2.20. The procedures +, *, and list take arbitrary numbers of arguments. One way to define such procedures is to use define with dotted-tail notation. In a procedure definition, a parameter list that has a dot before the last parameter name indicates that, when the procedure is called, the initial parameters (if any) will have as values the initial arguments, as usual, but the final parameter's value will be a list of any remaining arguments. For instance, given the definition
the procedure f can be called with two or more arguments. If we evaluate
then in the body of f, x will be 1, y will be 2, and z will be the list (3 4 5 6). Given the definition
the procedure g can be called with zero or more arguments. If we evaluate
then in the body of g, w will be the list (1 2 3 4 5 6).
Use this notation to write a procedure same-parity that takes one or more integers and returns a list of all the arguments that have the same even-odd parity as the first argument. For example,
Answer:
Exercise 2.21. The procedure square-list takes a list of numbers as argument and returns a list of the squares of those numbers.
Here are two different definitions of square-list. Complete both of them by filling in the missing expressions:
Answer:
Exercise 2.22. Louis Reasoner tries to rewrite the first square-list procedure of exercise 2.21 so that it evolves an iterative process:
Unfortunately, defining square-list this way produces the answer list in the reverse order of the one desired. Why?
Louis then tries to fix his bug by interchanging the arguments to cons:
This doesn't work either. Explain.
Answer: In the first procedure
iter starts by attaching the first item from the input list to answers. Subsequent items are consed to answers, thereby ending up *before* the first. Hence answers ends up having the square of the items in reverse order.
The second approach tried by Louis gets the order right. However the end result is not a plain list as he expects. Here the
cons operation starts by attaching the empty answer list to the square of the first item. This yields (() . 1) and not (1). Further iterations repeat the same operation with similar results.
Exercise 2.23. The procedure for-each is similar to map. It takes as arguments a procedure and a list of elements. However, rather than forming a list of the results, for-each just applies the procedure to each of the elements in turn, from left to right. The values returned by applying the procedure to the elements are not used at all -- for-each is used with procedures that perform an action, such as printing. For example,
The value returned by the call to for-each (not illustrated above) can be something arbitrary, such as true. Give an implementation of for-each.
Answer:
Exercise 2.24. Suppose we evaluate the expression (list 1 (list 2 (list 3 4))). Give the result printed by the interpreter, the corresponding box-and-pointer structure, and the interpretation of this as a tree (as in figure 2.6). Answer: The interpreter prints
(1 (2 (3 4))). I'll add the pictures once I draw them out using GIMP.
Exercise 2.25. Give combinations of cars and cdrs that will pick 7 from each of the following lists:
Answer:
Exercise 2.26. Suppose we define x and y to be two lists:
What result is printed by the interpreter in response to evaluating each of the following expressions:
Answer:
Exercise 2.27. Modify your reverse procedure of exercise 2.18 to produce a deep-reverse procedure that takes a list as argument and returns as its value the list with its elements reversed and with all sublists deep-reversed as well. For example,
Answer:
Exercise 2.28. Write a procedure fringe that takes as argument a tree (represented as a list) and returns a list whose elements are all the leaves of the tree arranged in left-to-right order. For example,
Answer:
Exercise 2.29. A binary mobile consists of two branches, a left branch and a right branch. Each branch is a rod of a certain length, from which hangs either a weight or another binary mobile. We can represent a binary mobile using compound data by constructing it from two branches (for example, using list):
A branch is constructed from a length (which must be a number) together with a structure, which may be either a number (representing a simple weight) or another mobile:
a. Write the corresponding selectors left-branch and right-branch, which return the branches of a mobile, and branch-length and branch-structure, which return the components of a branch.
b. Using your selectors, define a procedure total-weight that returns the total weight of a mobile.
c. A mobile is said to be balanced if the torque applied by its top-left branch is equal to that applied by its top-right branch (that is, if the length of the left rod multiplied by the weight hanging from that rod is equal to the corresponding product for the right side) and if each of the submobiles hanging off its branches is balanced. Design a predicate that tests whether a binary mobile is balanced.
d. Suppose we change the representation of mobiles so that the constructors are
How much do you need to change your programs to convert to the new representation?
Answer: a. As the mobile is represented as a list the selectors are straight forward to implement.
b. Calculation of total weight is made easier by an utility procedure which calculates the weight of a given branch. These procedure use mutual recursion to calculate the total weight of a given mobile.
c. The test to find out if a mobile is balanced can be similarly written with the help of an utility procedure to find out if its sub-mobiles are balanced.
d. Only the selectors need to be changed. For instance the
right-branch can use (cdr mobile) instead of (car (cadr mobile)).
Exercise 2.30. Define a procedure square-tree analogous to the square-list procedure of exercise 2.21. That is, square-list should behave as follows:
Define square-tree both directly (i.e., without using any higher-order procedures) and also by using map and recursion.
Answer:
Exercise 2.31. Abstract your answer to exercise 2.30 to produce a procedure tree-map with the property that square-tree could be defined as
Answer:
Exercise 2.32. We can represent a set as a list of distinct elements, and we can represent the set of all subsets of the set as a list of lists. For example, if the set is (1 2 3), then the set of all subsets is (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3)). Complete the following definition of a procedure that generates the set of subsets of a set and give a clear explanation of why it works:
Answer:
Exercise 2.33. Fill in the missing expressions to complete the following definitions of some basic list-manipulation operations as accumulations:
Answer:
Exercise 2.34. Evaluating a polynomial in x at a given value of x can be formulated as an accumulation. We evaluate the polynomial
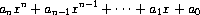
using a well-known algorithm called Horner's rule, which structures the computation as
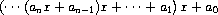
In other words, we start with an, multiply by x, add an-1, multiply by x, and so on, until we reach a0.16 Fill in the following template to produce a procedure that evaluates a polynomial using Horner's rule. Assume that the coefficients of the polynomial are arranged in a sequence, from a0 through an.
For example, to compute 1 + 3x + 5x3 + x5 at x = 2 you would evaluate
Answer:
Exercise 2.35. Redefine count-leaves from section 2.2.2 as an accumulation:
Answer:
Exercise 2.36. The procedure accumulate-n is similar to accumulate except that it takes as its third argument a sequence of sequences, which are all assumed to have the same number of elements. It applies the designated accumulation procedure to combine all the first elements of the sequences, all the second elements of the sequences, and so on, and returns a sequence of the results. For instance, if s is a sequence containing four sequences, ((1 2 3) (4 5 6) (7 8 9) (10 11 12)), then the value of (accumulate-n + 0 s) should be the sequence (22 26 30). Fill in the missing expressions in the following definition of accumulate-n:
Answer:
Exercise 2.37. Suppose we represent vectors v = (vi) as sequences of numbers, and matrices m = (mij) as sequences of vectors (the rows of the matrix). For example, the matrix
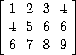
is represented as the sequence ((1 2 3 4) (4 5 6 6) (6 7 8 9)). With this representation, we can use sequence operations to concisely express the basic matrix and vector operations. These operations (which are described in any book on matrix algebra) are the following:

We can define the dot product as
Fill in the missing expressions in the following procedures for computing the other matrix operations. (The procedure accumulate-n is defined in exercise 2.36.)
Answer:
Exercise 2.38. The accumulate procedure is also known as fold-right, because it combines the first element of the sequence with the result of combining all the elements to the right. There is also a fold-left, which is similar to fold-right, except that it combines elements working in the opposite direction:
What are the values of
Give a property that op should satisfy to guarantee that fold-right and fold-left will produce the same values for any sequence.
Answer:
In order for
fold-right and fold-left to yield identical results op should be associative. For instance take the + operator.
Exercise 2.39. Complete the following definitions of reverse (exercise 2.18) in terms of fold-right and fold-left from exercise 2.38:
Answer:
Exercise 2.40. Define a procedure unique-pairs that, given an integer n, generates the sequence of pairs (i,j) with 1< j< i< n. Use unique-pairs to simplify the definition of prime-sum-pairs given above.
Answer:
Exercise 2.41. Write a procedure to find all ordered triples of distinct positive integers i, j, and k less than or equal to a given integer n that sum to a given integer s.
Answer:
Exercise 2.42.
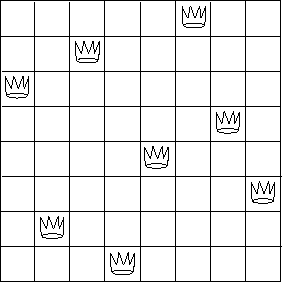
Figure 2.8: A solution to the eight-queens puzzle.
The ``eight-queens puzzle'' asks how to place eight queens on a chessboard so that no queen is in check from any other (i.e., no two queens are in the same row, column, or diagonal). One possible solution is shown in figure 2.8. One way to solve the puzzle is to work across the board, placing a queen in each column. Once we have placed k - 1 queens, we must place the kth queen in a position where it does not check any of the queens already on the board. We can formulate this approach recursively: Assume that we have already generated the sequence of all possible ways to place k - 1 queens in the first k - 1 columns of the board. For each of these ways, generate an extended set of positions by placing a queen in each row of the kth column. Now filter these, keeping only the positions for which the queen in the kth column is safe with respect to the other queens. This produces the sequence of all ways to place k queens in the first k columns. By continuing this process, we will produce not only one solution, but all solutions to the puzzle.
We implement this solution as a procedure queens, which returns a sequence of all solutions to the problem of placing n queens on an n× n chessboard. Queens has an internal procedure queen-cols that returns the sequence of all ways to place queens in the first k columns of the board.
In this procedure rest-of-queens is a way to place k - 1 queens in the first k - 1 columns, and new-row is a proposed row in which to place the queen for the kth column. Complete the program by implementing the representation for sets of board positions, including the procedure adjoin-position, which adjoins a new row-column position to a set of positions, and empty-board, which represents an empty set of positions. You must also write the procedure safe?, which determines for a set of positions, whether the queen in the kth column is safe with respect to the others. (Note that we need only check whether the new queen is safe -- the other queens are already guaranteed safe with respect to each other.)
Answer:
Exercise 2.43. Louis Reasoner is having a terrible time doing exercise 2.42. His queens procedure seems to work, but it runs extremely slowly. (Louis never does manage to wait long enough for it to solve even the 6× 6 case.) When Louis asks Eva Lu Ator for help, she points out that he has interchanged the order of the nested mappings in the flatmap, writing it as
Explain why this interchange makes the program run slowly. Estimate how long it will take Louis's program to solve the eight-queens puzzle, assuming that the program in exercise 2.42 solves the puzzle in time T.
Answer: Louis is breaking a well known rule of thumb in programming - namely to avoid expensive operations in inner loops. His code is calling the expensive recursive call to
queen-cols in the inner loop.
I am not able to figure out how much time Louis' procedure will take to run in terms of T. If you have an answer/explanation do let me know.



No comments:
Post a Comment