SICP Section 2.5 Systems with Generic Operations

Exercise 2.77. Louis Reasoner tries to evaluate the expression (magnitude z) where z is the object shown in figure 2.24. To his surprise, instead of the answer 5 he gets an error message from apply-generic, saying there is no method for the operation magnitude on the types (complex). He shows this interaction to Alyssa P. Hacker, who says ``The problem is that the complex-number selectors were never defined for complex numbers, just for polar and rectangular numbers. All you have to do to make this work is add the following to the complex package:''
(put 'real-part '(complex) real-part) (put 'imag-part '(complex) imag-part) (put 'magnitude '(complex) magnitude) (put 'angle '(complex) angle)
Describe in detail why this works. As an example, trace through all the procedures called in evaluating the expression (magnitude z) where z is the object shown in figure 2.24. In particular, how many times is apply-generic invoked? What procedure is dispatched to in each case?

Answer: After making Alyssa's changes a call to (magnitude z) will be dispatched to the magnitude method defined for complex types. On invoking this the actual magnitude method for rectangular representation is looked up and invoked. Hence the solution works.

Apply-generic is invoked twice. First when (magnitude z) is called; the next time when the magnitude method defined for rectangular implementation is called.

Exercise 2.78. The internal procedures in the scheme-number package are essentially nothing more than calls to the primitive procedures +, -, etc. It was not possible to use the primitives of the language directly because our type-tag system requires that each data object have a type attached to it. In fact, however, all Lisp implementations do have a type system, which they use internally. Primitive predicates such as symbol? and number? determine whether data objects have particular types. Modify the definitions of type-tag, contents, and attach-tag from section 2.4.2 so that our generic system takes advantage of Scheme's internal type system. That is to say, the system should work as before except that ordinary numbers should be represented simply as Scheme numbers rather than as pairs whose car is the symbol scheme-number.

Answer:
(define (attach-tag type-tag contents) (if (number? contents) contents (cons type-tag contents))) (define (type-tag datum) (if (number? datum) 'scheme-number (if (pair? datum) (car datum) (error "Bad tagged datum -- TYPE-TAG" datum)))) (define (contents datum) (if (number? datum) datum (if (pair? datum) (cdr datum) (error "Bad tagged datum -- CONTENTS" datum))))
Exercise 2.79. Define a generic equality predicate equ? that tests the equality of two numbers, and install it in the generic arithmetic package. This operation should work for ordinary numbers, rational numbers, and complex numbers.

Answer:
(define (equ? x y) (apply-generic 'equ? x y)) (define (install-scheme-number-equ) (put 'equ? '(scheme-number scheme-number) (lambda (x y) (= x y))) 'done) (define (install-rational-number-equ) (define (equal-rat? x y) (= (* (numer x) (denom y)) (* (numer y) (denom x)))) (put 'equ? '(rational rational) (lambda (x y) (equal-rat? x y))) 'done) (define (install-complex-number-equ) (define (equal-complex? x y) (and (= (magnitude x) (magnitude y)) (= (angle x) (angle y)))) (put 'equ? '(complex complex) (lambda (x y) (equal-complex? x y))) 'done)
Exercise 2.80. Define a generic predicate =zero? that tests if its argument is zero, and install it in the generic arithmetic package. This operation should work for ordinary numbers, rational numbers, and complex numbers.

Answer:
(define (=zero? x) (apply-generic '=zero? x)) (define (install-scheme-number-equ-zero) (put '=zero? '(scheme-number) (lambda (x) (= x 0))) 'done) (define (install-rational-number-equ-zero) (define (=zero? x) (= (numer x) 0)) (put '=zero? '(rational) (lambda (x) (=zero? x))) 'done) (define (install-complex-number-equ-zero) (define (=zero? x) (and (= (real-part x) 0) (= (imag-part x) 0))) (put '=zero? '(complex) (lambda (x) (=zero? x))) 'done)
Exercise 2.81. Louis Reasoner has noticed that apply-generic may try to coerce the arguments to each other's type even if they already have the same type. Therefore, he reasons, we need to put procedures in the coercion table to "coerce" arguments of each type to their own type. For example, in addition to the scheme-number->complex coercion shown above, he would do:
(define (scheme-number->scheme-number n) n) (define (complex->complex z) z) (put-coercion 'scheme-number 'scheme-number scheme-number->scheme-number) (put-coercion 'complex 'complex complex->complex)
a. With Louis's coercion procedures installed, what happens if apply-generic is called with two arguments of type scheme-number or two arguments of type complex for an operation that is not found in the table for those types? For example, assume that we've defined a generic exponentiation operation:
(define (exp x y) (apply-generic 'exp x y))
and have put a procedure for exponentiation in the Scheme-number package but not in any other package:
;; following added to Scheme-number package (put 'exp '(scheme-number scheme-number) (lambda (x y) (tag (expt x y)))) ; using primitive expt
What happens if we call exp with two complex numbers as arguments?

b. Is Louis correct that something had to be done about coercion with arguments of the same type, or does apply-generic work correctly as is?

c. Modify apply-generic so that it doesn't try coercion if the two arguments have the same type.

Answer: a. Louis' procedures doesn't help or add any new value with respect scheme numbers. His procedures actually create trouble in other cases - if apply-generic is called with two arguments of the same type for an operation that is not found in the table for those types, the procedure goes into an infinite loop.

b. Louis is incorrect; apply-generic is fine as is without his changes.

c. Changes to apply-generic:
(define (apply-generic op . args) (let ((type-tags (map type-tag args))) (let ((proc (get op type-tags))) (if proc (apply proc (map contents args)) (if (= (length args) 2) (let ((type1 (car type-tags)) (type2 (cadr type-tags)) (a1 (car args)) (a2 (cadr args))) (if (= type1 type2) (error "No method for these types" (list op type-tags)) (let ((t1->t2 (get-coercion type1 type2)) (t2->t1 (get-coercion type2 type1))) (cond (t1->t2 (apply-generic op (t1-t2 a1) a2)) (t2->t1 (apply-generic op a1 (t2->t1 a2))) (else (error "No method for these types" (list op type-tags))))))) (error "No method for these types" (list op type-tags)))))))
Exercise 2.83. Suppose you are designing a generic arithmetic system for dealing with the tower of types shown in figure 2.25: integer, rational, real, complex. For each type (except complex), design a procedure that raises objects of that type one level in the tower. Show how to install a generic raise operation that will work for each type (except complex).

Answer:
(define (install-generic-raise) (define (raise-integer i) (make-rat i 1)) (define (raise-rational r) (make-real (* (/ (numer r) (denom r)) 1.0))) (define (raise-real r) (make-from-real-imag r 0)) ;; interface (put '(integer) raise-integer) (put '(rational) raise-rational) (put '(real) raise-real) 'done) (define (raise number) (apply-generic 'raise number))
Exercise 2.84. Using the raise operation of exercise 2.83, modify the apply-generic procedure so that it coerces its arguments to have the same type by the method of successive raising, as discussed in this section. You will need to devise a way to test which of two types is higher in the tower. Do this in a manner that is ``compatible'' with the rest of the system and will not lead to problems in adding new levels to the tower.

Answer:
(define (apply-generic op . args) (define (raise-type s t) (let ((s-type (type-tag s)) (t-type (type-tag t))) (cond ((eq? s-type t-type) s) ((get 'raise (list s-type)) (raise-type ((get 'raise (list s-type)) (contents s)) t)) (else false)))) (let ((type-tags (map type-tag args))) (let ((proc (get op type-tags))) (if proc (apply proc (map contents args)) (if (= (length args) 2) (let ((type1 (car type-tags)) (type2 (cadr type-tags)) (a1 (car args)) (a2 (cadr args))) (if (= type1 type2) (error "No method for these types" (list op type-tags)) (cond ((raise-type type1 type2) (apply-generic op (raise-type type1 type2) type2)) ((raise-type type2 type1) (apply-generic op type1 (raise-type type2) type1)) (else (error "No method for these types" (list op type-tags)))))) (error "No method for these types" (list op type-tags)))))))
Exercise 2.85. This section mentioned a method for ``simplifying'' a data object by lowering it in the tower of types as far as possible. Design a procedure drop that accomplishes this for the tower described in exercise 2.83. The key is to decide, in some general way, whether an object can be lowered. For example, the complex number 1.5 + 0i can be lowered as far as real, the complex number 1 + 0i can be lowered as far as integer, and the complex number 2 + 3i cannot be lowered at all. Here is a plan for determining whether an object can be lowered: Begin by defining a generic operation project that ``pushes'' an object down in the tower. For example, projecting a complex number would involve throwing away the imaginary part. Then a number can be dropped if, when we project it and raise the result back to the type we started with, we end up with something equal to what we started with. Show how to implement this idea in detail, by writing a drop procedure that drops an object as far as possible. You will need to design the various projection operations53 and install project as a generic operation in the system. You will also need to make use of a generic equality predicate, such as described in exercise 2.79. Finally, use drop to rewrite apply-generic from exercise 2.84 so that it ``simplifies'' its answers.

Answer:
(define (install-type-projection) (define (project-complex->real c) (make-real (real-part c))) (define (project-real->rational r) (let ((ratio (inexact->exact r))) (make-real (numerator ratio) (denominator ratio)))) (define (project-rational->integer r) (round (/ (numer r) (denom r)))) (put 'project '(complex) project-complex->real) (put 'project '(real) project-real->rational) (put 'project '(rational) project-rational->integer) 'done) (define (project number) (apply-generic 'project number)) (define (drop x) (let ((projection (project x))) (if (not projection) x (if (equ? (raise projection) x) (drop projection) x)))) (define (apply-generic op . args) (define (raise-type s t) (let ((s-type (type-tag s)) (t-type (type-tag t))) (cond ((eq? s-type t-type) s) ((get 'raise (list s-type)) (raise-type ((get 'raise (list s-type)) (contents s)) t)) (else false)))) (let ((type-tags (map type-tag args))) (let ((proc (get op type-tags))) (if proc (drop (apply proc (map contents args))) ;; Only change. (if (= (length args) 2) (let ((type1 (car type-tags)) (type2 (cadr type-tags)) (a1 (car args)) (a2 (cadr args))) (if (= type1 type2) (error "No method for these types" (list op type-tags)) (cond ((raise-type type1 type2) (apply-generic op (raise-type type1 type2) type2)) ((raise-type type2 type1) (apply-generic op type1 (raise-type type2) type1)) (else (error "No method for these types" (list op type-tags)))))) (error "No method for these types" (list op type-tags)))))))
Exercise 2.87. Install =zero? for polynomials in the generic arithmetic package. This will allow adjoin-term to work for polynomials with coefficients that are themselves polynomials.

Answer:
(define (install-poly-equal-zero) (define (=zero-poly? poly) (define (zero-terms? terms) (and (=zero? (coeff (first-term terms))) (zero-terms? (rest-terms terms)))) (or (empty-termlist? (term-list poly)) (zero-terms? (term-list poly)))) (put '=zero? '(polynomial) (lambda (p) (=zero-poly? p))) 'done)
Exercise 2.88. Extend the polynomial system to include subtraction of polynomials. (Hint: You may find it helpful to define a generic negation operation.)

Answer:
(define (install-number-negation) (define (negate-integer i) (- 0 i)) ;; interface (put 'negate '(integer) (lambda (i) (negate-integer i))) 'done) (define (negate i) (apply-generic 'negate i)) (define (install-poly-negation) (define (negate-terms terms) (if (empty-termlist? terms) terms (let ((first (first-term terms)) (rest (rest-terms terms))) (adjoin-terms (make-term (order first) (negate (coeff first))) (negate-terms rest))))) (define (negate-poly poly) (make-poly (variable poly) (negate-terms (terms poly)))) (define (subtract-poly p1 p2) (add-poly p1 (negate p2))) (put 'negate '(polynomial) (lambda (p) (negate-poly p))) (put 'sub '(polynomial polynomial) (lambda (p1 p2) (tag (subtract-poly p1 p2)))) 'done)
Exercise 2.89. Define procedures that implement the term-list representation described above as appropriate for dense polynomials.

Answer:
(define (adjoin-term term term-list) (define (pad-zero seq expected-length) (if (= expected-length (length seq)) seq (pad-zero (cons 0 seq) expected-length))) (define (add-terms S1 S2) (accumulate-n + 0 (list S1 S2))) (let ((L1 (length term)) (L2 (length term-list))) (cond ((= L1 L2) (add-terms term term-list)) ((> L1 L2) (add-terms term (pad-zero term-list L1))) (else (add-terms (pad term L2) term-list)))))
Exercise 2.91. A univariate polynomial can be divided by another one to produce a polynomial quotient and a polynomial remainder. For example,



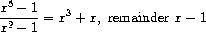
Division can be performed via long division. That is, divide the highest-order term of the dividend by the highest-order term of the divisor. The result is the first term of the quotient. Next, multiply the result by the divisor, subtract that from the dividend, and produce the rest of the answer by recursively dividing the difference by the divisor. Stop when the order of the divisor exceeds the order of the dividend and declare the dividend to be the remainder. Also, if the dividend ever becomes zero, return zero as both quotient and remainder.

We can design a div-poly procedure on the model of add-poly and mul-poly. The procedure checks to see if the two polys have the same variable. If so, div-poly strips off the variable and passes the problem to div-terms, which performs the division operation on term lists. Div-poly finally reattaches the variable to the result supplied by div-terms. It is convenient to design div-terms to compute both the quotient and the remainder of a division. Div-terms can take two term lists as arguments and return a list of the quotient term list and the remainder term list.

Complete the following definition of div-terms by filling in the missing expressions. Use this to implement div-poly, which takes two polys as arguments and returns a list of the quotient and remainder polys.
(define (div-terms L1 L2) (if (empty-termlist? L1) (list (the-empty-termlist) (the-empty-termlist)) (let ((t1 (first-term L1)) (t2 (first-term L2))) (if (> (order t2) (order t1)) (list (the-empty-termlist) L1) (let ((new-c (div (coeff t1) (coeff t2))) (new-o (- (order t1) (order t2)))) (let ((rest-of-result <compute rest of result recursively> )) <form complete result> ))))))
Answer:
(define (div-terms L1 L2) (if (empty-termlist? L1) (list (the-empty-termlist) (the-empty-termlist)) (let ((t1 (first-term L1)) (t2 (first-term L2))) (if (> (order t2) (order t1)) (list (the-empty-termlist) L1) (let ((new-c (div (coeff t1) (coeff t2))) (new-o (- (order t1) (order t2)))) (let ((rest-of-result (let ((new-term (make-term new-o new-c)) (let ((product (add L1 (negate (mul-terms (list new-term) L2))))) (div-terms product L2)))))) (list (cons new-term (car rest-of-result)) (cadr res-of-result)))))))) (define (div-poly P1 P2) (if (same-variable? P1 P2) (let ((L1 (term-list P1)) (L2 (term-list P2))) (let ((result (div-terms L1 L2))) (list (make-poly (variable P1) (car result)) (make-poly (variable P1) (cadr result))))) (error "Polys are not in the same variable -- DIV-POLY" (list P1 P2))))
Exercise 2.94. Using div-terms, implement the procedure remainder-terms and use this to define gcd-terms as above. Now write a procedure gcd-poly that computes the polynomial GCD of two polys. (The procedure should signal an error if the two polys are not in the same variable.) Install in the system a generic operation greatest-common-divisor that reduces to gcd-poly for polynomials and to ordinary gcd for ordinary numbers. As a test, try
(define p1 (make-polynomial 'x '((4 1) (3 -1) (2 -2) (1 2)))) (define p2 (make-polynomial 'x '((3 1) (1 -1)))) (greatest-common-divisor p1 p2)
and check your result by hand.

Answer:
(define (gcd-terms a b) (if (empty-termlist? b) a (gcd-terms (remainder-terms a b)))) (define (remainder-terms a b) (cadr (div-terms a b))) (define (gcd-poly P1 P2) (if (same-variable P1 P2) (make-poly (variable P1) (gcd-terms (term-list P1) (term-list P2))) (error "Polys are not in the same variable -- GCD-POLY" (list P1 P2))))
Exercise 2.96. a. Implement the procedure pseudoremainder-terms, which is just like remainder-terms except that it multiplies the dividend by the integerizing factor described above before calling div-terms. Modify gcd-terms to use pseudoremainder-terms, and verify that greatest-common-divisor now produces an answer with integer coefficients on the example in exercise 2.95.

b. The GCD now has integer coefficients, but they are larger than those of P1. Modify gcd-terms so that it removes common factors from the coefficients of the answer by dividing all the coefficients by their (integer) greatest common divisor.

Thus, here is how to reduce a rational function to lowest terms:

• Compute the GCD of the numerator and denominator, using the version of gcd-terms from exercise 2.96.,
• When you obtain the GCD, multiply both numerator and denominator by the same integerizing factor before dividing through by the GCD, so that division by the GCD will not introduce any noninteger coefficients. As the factor you can use the leading coefficient of the GCD raised to the power 1 + O1 - O2, where O2 is the order of the GCD and O1 is the maximum of the orders of the numerator and denominator. This will ensure that dividing the numerator and denominator by the GCD will not introduce any fractions.
• The result of this operation will be a numerator and denominator with integer coefficients. The coefficients will normally be very large because of all of the integerizing factors, so the last step is to remove the redundant factors by computing the (integer) greatest common divisor of all the coefficients of the numerator and the denominator and dividing through by this factor.

Answer:
;; a (define (pseudoremainder-terms a b) (let ((O1 (order (first-term a))) (O2 (order (first-term b))) (C (coeff (first-term a)))) (let ((i-factor (exp C (+ 1 (- O1 O2))))) (cadr (div-terms (map (lambda (t) (make-term (order t) (* i-factor (coeff t)))) a) b))))) (define (gcd-terms a b) (if (empty-termlist? b) a (gcd-terms b (pseudoremainder-terms a b))))